Процесс проецирования можно рассматривать как преобразование точки (х, у, z) в другую точку (хг. ур, zp). Это перспективное преобразование (perspective transformation)
5.3. Проецирование сохраняет линейность, но не является аффинным. Кроме того, оно необратимо. Поскольку все точки, расположенные на проецирующем луче, преобразуются в одну и ту же точку, восстановить их исходное положение нельзя2. Для работы с проективными преобразованиями нам придется слегка модифицировать используемый аппарат однородных координат.
При описании однородных координат мы представляли трехмерную точку (х, у, г) в виде четырехмерной (х, у, г, 1). Вместо этого будем представлять точку (х, у, г) в таком виде:
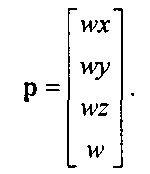
Если м> * 0, то трехмерное представление точки можно однозначно восстановить из четырехмерного, разделив три первых компонента на четвертый и». В этой более общей форме однородных координат трехмерные точки отображаются в прямые четырехмерного пространства. Преобразования по-прежнему выражаются матрицами размера 4x4, но теперь элементы последней строки можно изменять, и, таким образом, преобразование распространяется и на четвертый компонент м>.
Естественно, мы будем стараться работать с \\> = 1, поскольку это позволяет избежать дополнительных операций деления при восстановлении трехмерных координат. Однако, изменяя и>, можно представить в матричном виде более широкий класс преобразований, в том числе и перспективное. Рассмотрим матрицу
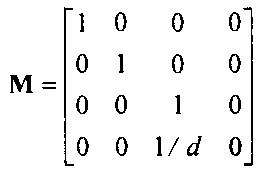
Матрица М преобразует точку
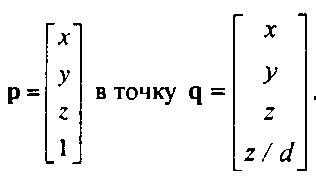
На первый взгляд в q мало что изменилось по сравнению с р, но не нужно забывать, что при переходе в трехмерное пространство первые три компонента необходимо разделить на четвертый. Следовательно, получится результат
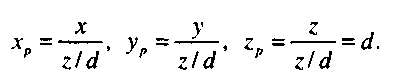
Приведенные уравнения описывают простое перспективное преобразование. В однородных координатах деление компонентов точки q на четвертый компонент м> заменяет ее эквивалентной точкой:
2В разделах 5.7 и 5.8 будет рассказано об обратимом варианте проецирующего преобразования, который реализован в OpenGL.
