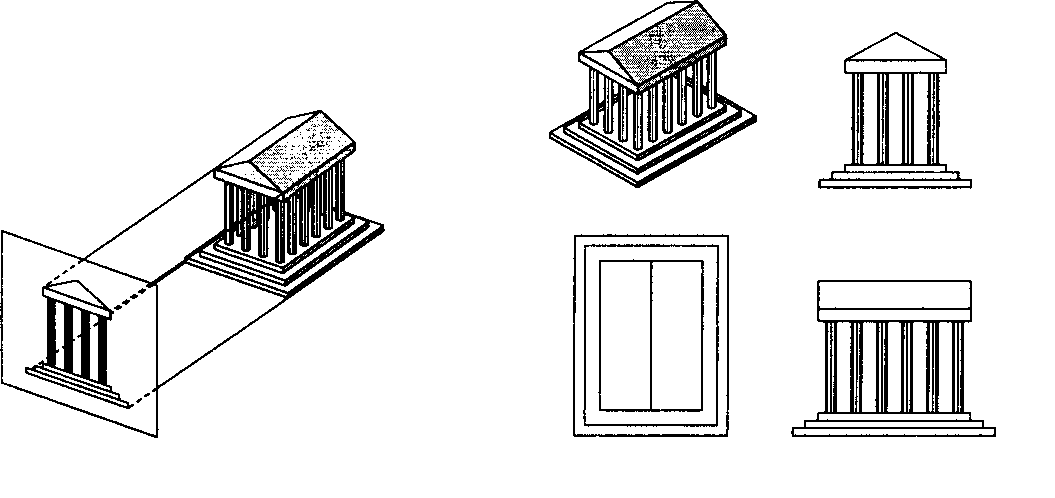
Рис. 5.4. Ортографическая проекция Рис. 5.5. Здание и три его ортогональных вида
5.1.3. Аксонометрические проекции Если желательно иметь на чертеже изображение не одной главной грани, а двух-трех, нужно устранить одно из ограничений, характеризующих ортографические проекции. В аксонометрических (axonometric) проекциях проецирующие лучи по-прежнему ортогональны картинной плоскости, как показано на рис. 5.6, но сама картинная плоскость может иметь любую ориентацию относительно объекта. Если картинная плоскость ориентирована симметрично по отношению к трем главным граням, пересекающимся в одном углу прямоугольного объекта, то образуется изометрическая (isometric) проекция. Если картинная плоскость ориентирована симметрично по отношению к двум главным граням, то образуется диметри-ческая (dimetric) проекция. Общий случай - триметрическая (trimetric) проекция. Все три вида аксонометрических проекций показаны на рис. 5.7. Обратите внимание на то, что на изометрическом виде длины отрезков меньше, чем на исходном объекте. В изометрической проекции коэффициент искажения (foreshortening) длин одинаков по всем трем главным осям, а потому такой вид можно использовать для измерения длин. В диметрической проекции коэффициент искажения длин по двум осям одинаков, а по третьей отличается, т.е. мы имеем дело с парой коэффициентов. В триметрической проекции коэффициенты искажения по всем трем осям различны. В аксонометрических проекциях сохраняется параллельность прямых, но углы между ними искажаются. Окружность в аксонометрической проекции пре-
Визуализация
образуется в эллипс. Эти искажения - плата за возможность видеть на одной плоской проекции больше, чем одну главную грань объекта, при том что методы построения аксонометрических проекций достаточно просты и давно освоены в техническом черчении. Аксонометрические проекции широко применяются в архитектурном планировании и техническом конструировании.
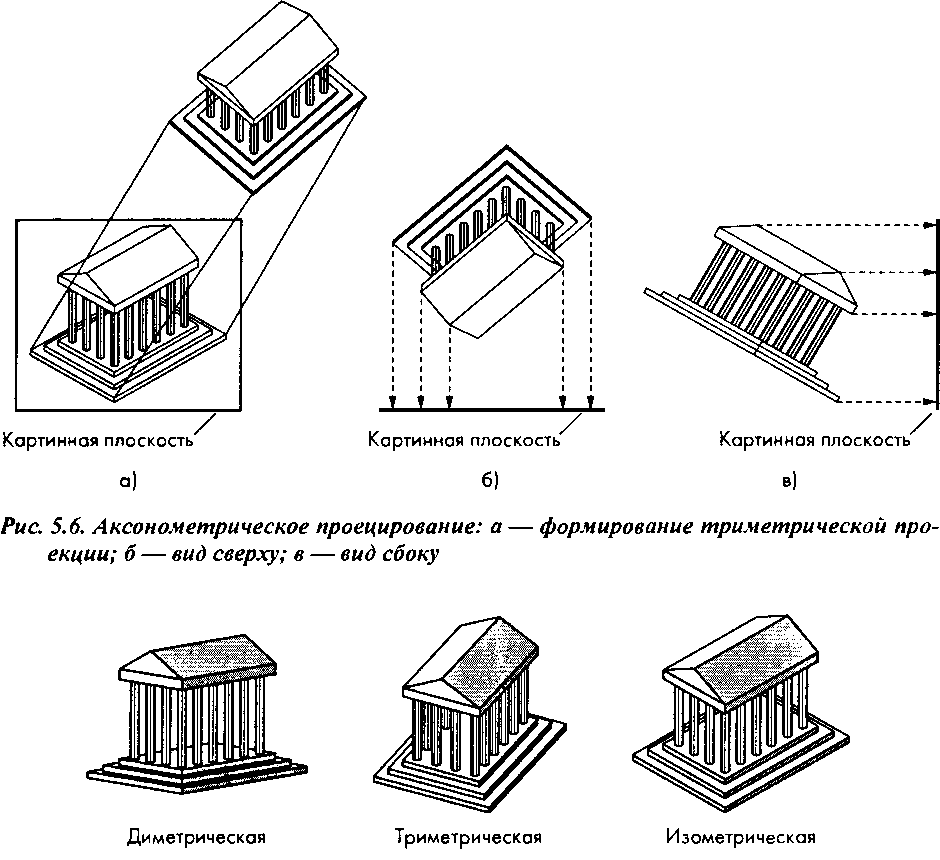
Рис. 5.7. Виды аксонометрических проекций
5.1.4. Косоугольные проекции Косоугольная (oblique) проекция является параллельной проекцией общего вида. При построении косоугольной проекции не накладываются никакие ограничения на угол между проецирующими лучами и картинной плоскостью (рис. 5.8). В косоугольной проекции сохраняются углы между прямыми на объекте, расположенными в плоскости, параллельной картинной. Окружность в такой плоскости также проецируется в окружность и при этом на изображении присутствует более чем одна главная грань объекта. Строить косоугольные проекции вручную - задача довольно сложная. Кроме того, они выглядят все-таки как-то ненатурально. В большинстве физических систем формирования изображения - в фотоаппаратах или в глазах человека- плоскость объектива параллельна картинной плоскости. Хотя в таких приборах фактически формируется перспективная проекция, но при разглядывании достаточно удаленных объектов получается почти параллельная проекция, но именно ортогонально параллельная, поскольку картинная плоскость параллельна плоскости объектива. Не-
