Объекты и геометрические преобразования
торая выполняет преобразование. Если посчитать количество операций, то окажется, что вычисление матрицы М требует несколько большего числа операций, чем (С(В(Ар))), но затем при обработке каждой из сотен или тысяч точек требуется выполнить только одну операцию умножения квадратной матрицы на матрицу-столбец. Ниже на примерах будет показано, как вычислять матрицу М.
Рис. 4.40. Выполнение преобразований в графическом конвейере
4.8.1. Поворот вокруг произвольной фиксированной точки В первом примере будет показано, как формировать матрицу преобразований поворота вокруг произвольной фиксированной точки, используя канонические матрицы поворота вокруг начала координат. Направление оси поворота в примере совпадает с направлением координатной оси г, но этот же метод можно использовать и при другом направлении оси.
Рассмотрим куб, центр которого находится в точке р/, а ребра параллельны осям координат. Требуется повернуть куб вокруг оси 2, но сохранить неизменным положение центра (рис. 4.41). Если бы точка р^ совпадала с началом координат, мы могли бы воспользоваться уже сформированной матрицей К.(9). Отсюда следует, что сначала нужно сдвинуть куб таким образом, чтобы его центр оказался в начале координат, а затем воспользоваться матрицей Кг(в). Последняя операция - сдвинуть куб так, чтобы его центр занял прежнее положение р/. Эта последовательность преобразований представлена на рис. 4.42. Используя введенные раньше обозначения, нужно сначала выполнить преобразование Т(-ру), далее - К.(Э), а последним выполнить Т(р^). В результате суперпозиции этих преобразований получим матрицу
М = Т(Р/)Кг(в)Т(-Р/).
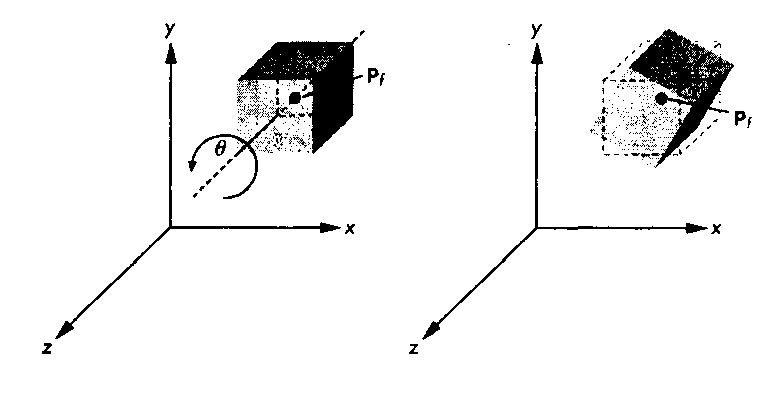
а) 6) Рис 4.41. Поворот куба вокруг собственного центра После перемножения матриц получим"images/tmpB6CA-140.png">
4.8. Суперпозиция преобразований
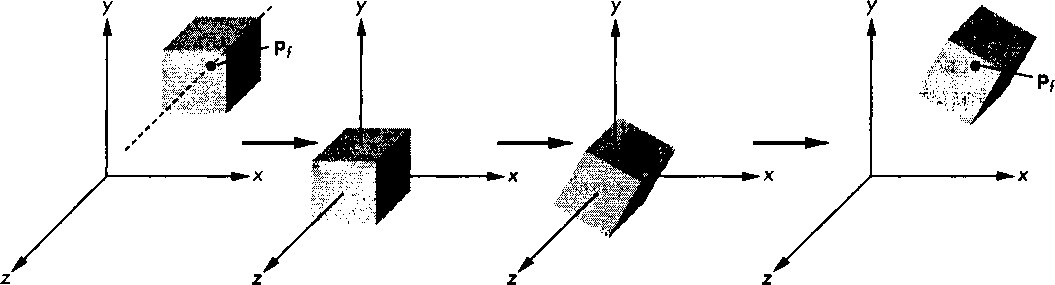
Рис. 4.42. Последовательность канонических преобразований
4.8.2. Поворот вокруг произвольной оси Теперь покажем, как можно представить поворот вокруг произвольной оси в виде суперпозиции трех поворотов вокруг осей координат. Порядок выполнения канонических преобразований в этом случае не однозначен (см. упр. 4.10), хотя результат будет однозначным. В примере начало координат выбрано в качестве фиксированной точки преобразования. Первой операцией будет поворот вокруг оси г, затем поворот вокруг оси у и последним - поворот вокруг оси X.
