"1 ctg0 О О"

0 10 0
0 0 10
0 0 0 1

Н,(0) =

Матрицу обратного преобразования несложно получить, если учесть, что следует выполнить скос в обратном направлении; следовательно, Н, '(9) = нД-8).

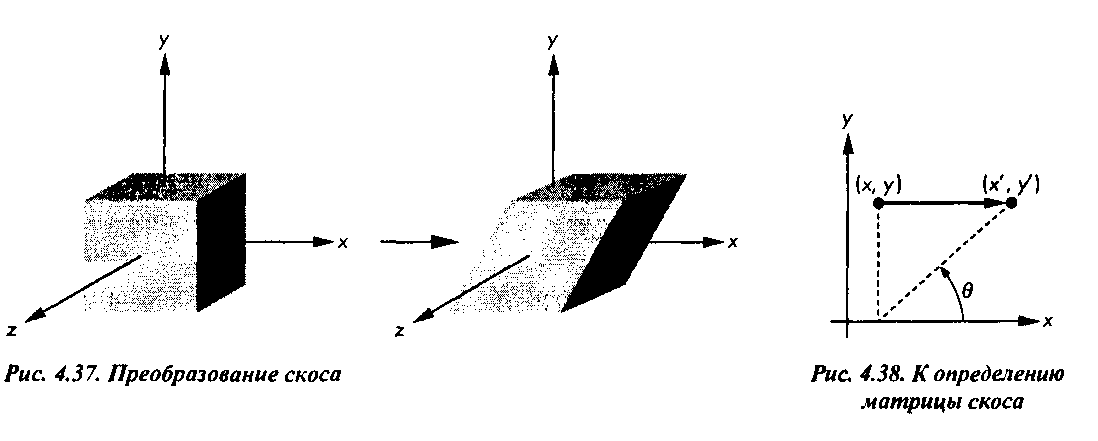
4.7. Преобразования в однородных координатах

4.8. Суперпозиция преобразований В этом разделе продемонстрировано, как формировать матрицу сложного аффинного преобразования, перемножая матрицы отдельных базовых (канонических) преобразований. Выражаясь языком математики, можно сказать, что сложное преобразование есть суперпозиция базовых преобразований (concatenating), которые были рассмотрены в предыдущем разделе. Использованию такой стратегии формирования матрицы сложного преобразования следует отдать предпочтение перед непосредственным вычислением элементов матрицы. Этот подход хорошо "вписывается" в конвейерную архитектуру графической системы.

Предположим, что выполняются три последовательных преобразования точки р и при этом формируется новая точка q. Поскольку произведение матриц ассоциативно, можно записать такую последовательность преобразований в виде

q = СВАр, без использования скобок. Однако порядок выполнения операций существенно влияет на производительность процесса вычисления. Например, можно сначала умножить матрицу А, затем на полученный результат умножить матрицу В, а потом умножить матрицу С (этот порядок соответствует группировке, представленной на рис. 4.39):

q = (C(B(Ap))).

Рис 4.39. Последовательное выполнение преобразований Если выполняется преобразование единственной точки, то этот порядок наиболее эффективен, поскольку на каждом шаге квадратная матрица умножается на матрицу-столбец. Но если необходимо преобразовать множество точек, то операцию следует реализовать в два этапа. Сначала вычислять произведение квадратных матриц отдельных преобразований"opengl5_204.html">⇐ Предыдущая| |Следующая ⇒