Как видно на рис. 4.35, преобразование масштабирования также имеет фиксированную точку. Таким образом, набор параметров этого преобразования включает фиксированную точку, направление, вдоль которого изменяется масштаб, и масштабный множитель (а). При а > 1 объект растягивается в заданном направлении, а при 0 < а <1 объект сжимается. При отрицательном значении а происходит отражение (reflection) объекта относительно заданной фиксированной точки в указанном направлении (рис. 4.36).

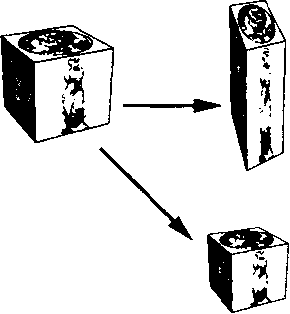
Рис. 4.34. Пропорциональное и неравномерное масштабирование

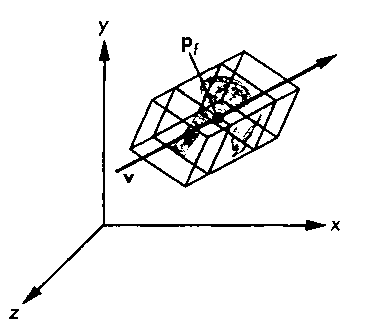
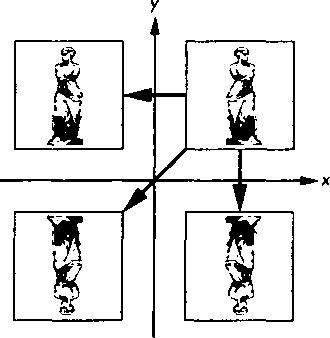
Рис. 4.35. Параметры масштабирования Рис. 4.36. Отражение

4.6. Поворот, сдвиг и масштабирование

4.7. Преобразования в однородных координатах

В большинстве графических АРІ приходится работать в определенной системе отсчета (системе координат). Хотя программист и может изменить эту систему координат (как правило, фрейм), он не может работать с представлениями на высоком уровне, например с выражениями вида

£ = Р + ау.

Вместо этого программист имеет дело с представлениями в однородных координатах и выражениями вида Я = р + с/у.

В некотором фрейме любое аффинное преобразование может быть представлено матрицей 4x4 вида А =

4.7.1. Сдвиг Преобразование сдвига смещает точки в новые позиции в соответствии с заданным вектором смещения. Если точка р сдвигается в р' на расстояние с1, то такое преобразование можно записать в виде р' = р + (1.

В однородных координатах р, р' и (1 выражаются следующим образом"box" rules="all" border="1"> X

х'

а,

У

. Р' =

у'

, а =

а3

Тогда эти уравнения можно записать в виде отдельных выражений для каждого компонента: х' = х+ а*, у' = У + Оу, 2'= 2 + 0..

Метод представления преобразования сдвига посредством суммирования матриц-столбцов плохо сочетается с другими аффинными преобразованиями. Существует и другой метод представления сдвига - с помощью перемножения матриц:

⇐ Предыдущая| |Следующая ⇒