4.6.2. Поворот
Задать поворот (rotation) несколько сложнее, чем сдвиг, так как требуется специфицировать больше параметров. Начнем с простого примера поворота точки вокруг начала координат в двухмерной плоскости, как показано на рис. 4.30. Поскольку задана определенная точка - начало координат, - мы имеем дело с определенным фреймом. Двухмерная точка (д:, у) в этом фрейме поворачивается вокруг начала координат на угол 6 и занимает после поворота позицию (х', у'). Формулы описания поворота несложно получить, воспользовавшись полярным представлением точек (х, у) и (х', уу.
X = р COS0, у = р sin<)>, x'=pcos(6 + ф), У - р sin(8 + ф).
Воспользовавшись формулами приведения синуса и косинуса суммы углов, получим х' = р соБф cosG - р вшф sinO = х cosG-у sine, у'-р соБф sin9 + р Бшф cosO = х sin9 + у cosG.
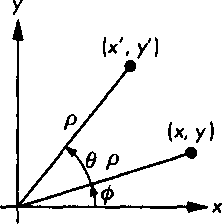
Рис 4.30. Поворот в двухмерной системе координат
4.6. Поворот, сдвиг и масштабирование Эти же уравнения можно записать и в матричной форме"images/tmpB6CA-129.png">
О том, как можно расширить эти формулы на трехмерный случай, вы узнаете в разделе 4.7.
Обратите внимание на три свойства этого преобразования, которые сохраняются и в других вариантах операции поворота.
1. Существует некоторая точка, она называется фиксированной точкой (fixed point) преобразования (в приведенном выше примере- начало координат), которая остается неподвижной при применении к ней этого преобразования. На рис. 4.31 показано, какой результат получится при повороте вокруг фиксированной точки, отличной от начала координат.
2. Учитывая, что двухмерное пространство является частным случаем трехмерного, можно распространить сделанные выводы и на три измерения. В правосторонней системе координат, когда оси х и у выглядят привычным для всех нас образом, положительное направление оси z трехмерной системы координат будет направлено на наблюдателя (т.е. ось z "исходит" из листа бумаг, на котором начерчены оси х и у). Положительное направление поворота - это направление против часовой стрелки, если смотреть со стороны положительной полуоси г, исходящей из фиксированной точки. Это же определение положительного направления поворота мы будем использовать и для трехмерного случая при повороте вокруг произвольной оси.
