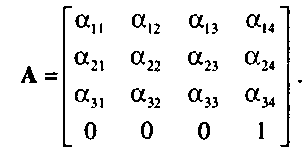
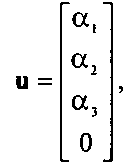
9Рассматриваются только такие функции преобразования, которые отображают одни вершины на другие вершины и которые подчиняются правшам манипулирования с точками и векторами, описанными ранее в этой главе и в приложении Б.
4.5. Аффинные преобразования а любую точку - в виде
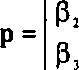
Если рассмотреть применение произвольного преобразования А по отношению к вектору V = Аи, то придем к выводу, что на результат влияют только 9 элементов матрицы А, т.е. преобразование векторов обладает только девятью степенями свободы. Аффинные преобразования точек обладают всеми двенадцатью степенями свободы.
Несложно показать, что аффинное преобразование преобразует прямую линию в прямую линию. Предположим, что прямая линия записана в виде Да) = Р0 + оА, где Р0 - точка, ас/ - вектор. В некотором фрейме прямая выражается с помощью представления р0 и (1 соответственно, точки Р0 и вектора в этом фрейме: р(а) = р0 + ас1.
Для любой матрицы аффинного преобразования А справедливо соотношение Ар(сс) = Ар0 + а Ад.
Таким образом, можно построить преобразование прямой, выполнив сначала преобразование р0 и (1, а затем воспользоваться любым алгоритмом формирования прямой. Если используется форма представления отрезка двумя точками р(а) = ар0 + (1-<х)р1, получим аналогичный результат- нужно сначала выполнить преобразование р0 и р(, а затем по ним построить преобразованный отрезок. Поскольку в матрице А имеется 12 элементов, которые можно выбирать произвольно, то аффинное преобразование прямой или прямолинейного отрезка имеет 12 степеней свободы.
До сих пор мы рассуждали в терминах абстрактного математического пространства. Однако эти рассуждения имеют совершенно конкретное приложение к практическим проблемам компьютерной графики. Из них следует, что для построения в системе компьютерной графики изображения преобразованного отрезка необходимо выполнить только преобразование представлений в однородных координатах конечных точек этого отрезка, а, следовательно, графическую систему можно реализовать в виде конвейера аффинных преобразований представлений отдельных точек в однородных координатах.
