Объекты и геометрические преобразования

с началом вектора В и сформирован новый вектор С, величина и направление которого определяются отрезком, соединяющим начало вектора А и конец вектора В. Этот новый вектор будем называть суммой векторов А и В и записывать соотношение между ними в виде С=А+В. Обратите внимание на то, что поскольку векторы не имеют фиксированной точки приложения, то для геометрического сложения векторов их можно переносить параллельно самим себе куда угодно.

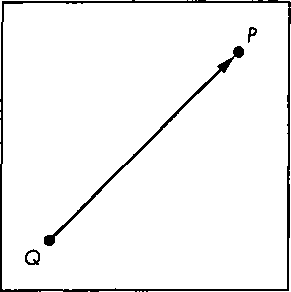
Рис. 4.1. Соединение двух точек направленным отрезком Рис. 4.2. Одинаковые векторы

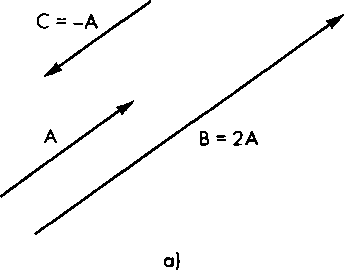
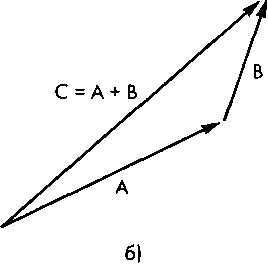
Рис. 4.3. Соотношение между векторами: а - выраженное с помощью вещественных чисел; б - правило сочленения начала с концом Точки и векторы - это разные геометрические типы. Геометрическое представление точки в виде направленного отрезка, соединяющего некоторую опорную точку с заданной (рис. 4.4), следует рассматривать как сомнительное. Однако существует операция, в которой связываются точки и направленный отрезок (см. рис. 4.1.) Можно использовать направленный отрезок для перемещения от одной точки к другой. Точно так же две точки определяют отрезок, проведенный между ними, а точка и вектор определяют вторую точку. Таким образом, правильная интерпретация рис. 4.4 состоит в том, что данный вектор можно определить как исходящий из фиксированной опорной точки (начала системы координат) и приходящий в определенную точку пространства. Обратите внимание на то, что вектор, как и точка, существует независимо от опорной системы, но, как будет показано дальше, мы должны будем работать с их представлениями в определенной систе ме координат.

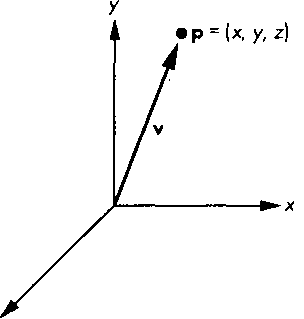
Рис. 4.4. Сомнительное представление вектора

4.1. Скаляры, точки и векторы

4.1.2. Математическое определение"opengl5_167.html">⇐ Предыдущая| |Следующая ⇒