2.11. В разделе 2.3 при анализе положения точки относительно контура многоугольника были проигнорированы проблемы, которые могут возникнуть, если одна или несколько сторон многоугольника окажутся параллельными линиям растра. В чем, по-вашему, суть этих проблем? Как с ними справиться?
2.12. С практической точки зрения анализ каждой точки некоторой области на принадлежность внутренней или внешней области многоугольника крайне неэффективен. Разработайте общую стратегию, которой нужно следовать, чтобы избежать анализа всего массива точек.
2.13. В разделе 2.3 было сказано, что в OpenGL многоугольник задается списком его вершин. Как можно в рамках системы OpenGL задать многоугольник его ребрами?
2.14. Разработайте тест простоты многоугольника.
2.15. На рис. 2.42 показано множество многоугольников, образующее полигональную сеть {polygonal mesh). Эти многоугольники имеют совместные грани и вершины. Разработайте один или несколько вариантов структур данных, описывающих такую сеть. "Хорошая" структура данных должна включать информацию о совместном использовании вершин и ребер. В рамках системы OpenGL отыщите эффективный метод отображения сети, представленной такой структурой.
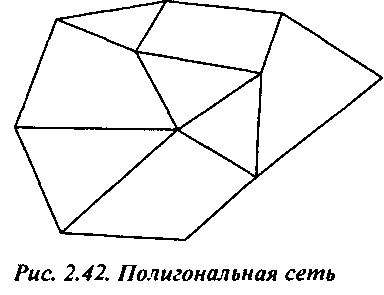
Графическое программирование
2.16. В системе OpenGL с каждой вершиной можно связать некоторый цвет. Если вершины отрезка имеют разные цвета, OpenGL при вычерчивании отрезка плавно изменяет (интерполирует) цвет линии по мере перемещения от начальной вершины к конечной. Точно так же вычерчиваются и ребра многоугольников. Воспользуйтесь этим свойством OpenGL и разработайте программу вычерчивания треугольника Максвелла (Maxwell triangle)- равностороннего треугольника, вершины которого имеют красный, зеленый и синий цвета. Как соотносятся треугольник Максвелла и цветовой куб?
2.17. Включив в модель описание некоторых физических явлений, можно получить довольно интересные изобразительные эффекты. Смоделируйте прыгающий шарик в двухмерном пространстве, используя явления гравитации и упругого столкновения с поверхностью. Сам шарик можно представить в виде замкнутого многоугольника с достаточно большим количеством сторон, чтобы он выглядел на экране как гладкий.
