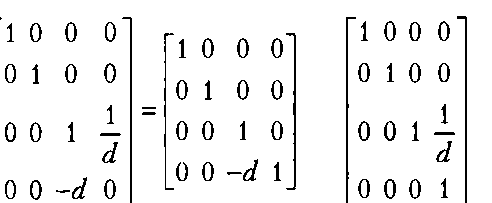
(24.10).Теперь нужно проверить, как объединенная матрица переноса и проецирования изменяет координату г.
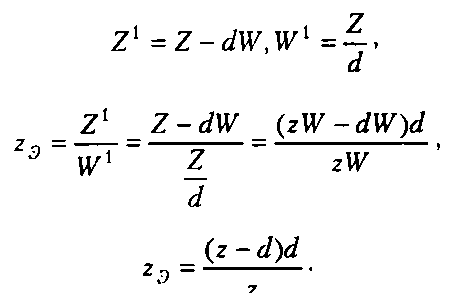
При 2 = йг, получает нулевое значение, а при максимальном значении г - /
_(/-<№Таким образом, чтобы для всех точек пирамиды видимости координата г, после умножения на произведение (24.8) находилась в интервале (0,1), полученный результат нужно умножить на масштабный коэффициент
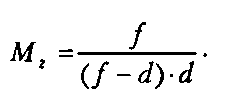
Параллелепипед, полученный из пирамиды данным преобразованием, имеет в плоскости ХУ размеры 1УхЯ. Чтобы координаты (х9, уэ) привести к диапазону (-1, 1), нужно для масштабных коэффициентов Мх, Му установить значения 2/IV, 2/Н.
Геометрические преобразования
После умножения на матрицу масштабирования получим выражение.
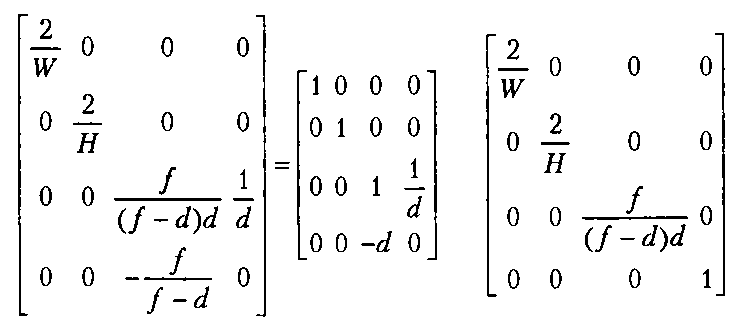
(24.11).Все элементы матрицы (24.11) меньше единицы. Для уменьшения вычислительной погрешности нужно умножить все элементы на в,. Численную матрицу можно получить, подставив значения \¥, Н, г/,/из постановки задачи.
Для уменьшения объема вычислений проектировщик может назначить ближнюю границу видимости дальше плоскости экрана. Так, в нашей сцене экран находится на расстоянии метра от камеры, а требуется, чтобы отсекались и пропадали с экрана все объекты ближе полутора метров. Для задания ближней границы видимости отдельного механизма не предусмотрено. Просто надо считать экранной плоскостью ближнюю грань пирамиды видимости и пропорционально отношению увеличить размеры И^иЯ. Полученное окончательное значе ние (4.11) уже трудно назвать матрицей проецирования, правильнее называть ее матрицей приведения пирамиды видимости к каноническому объему:
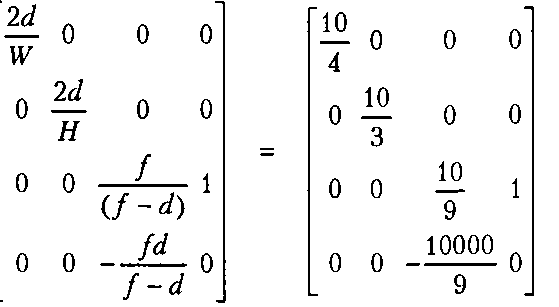
(24.12).Нужно проверить правильность матрицы на численных значениях, заданных при постановке задачи, когда наблюдатель находится в начальном положении. Умножая координаты (X, У, 1,1) на матрицу (24.12) можно получить однородные координаты (2.5Х, 10У/3, 102/9 - 10000/9, Г).
Можно получить и соответствующие декартовы координаты:
* - 2.5х/г,у9 - (юу/зуг, г9 - (юг/9-юооо/9)/г.
Точка на дальней границе видимости действительно имеет координату гэ. = (100000/9 - 10000/9)/10000 = 1, а точка экранной плоскости обладает нулевой координатой 2Э.
