Выражение (24.8) усложняет организацию взаимодействия пользователя с объектами модельного мира. Для этого может потребоваться применять матрицу, обратную матрице геометрических преобразований, для восстановления мировых координат точки по ее проекционным координатам. Матрица (24.8) имеет нулевой определитель и не обеспечит восстановления координат.
Следует заметить, что в приведенных выражениях численное значение координаты У/ получается пропорциональным глубине 2, поэтому ее вполне можно
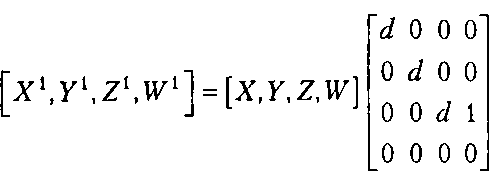
(24.7).Геометрические преобразования
использовать в алгоритме удаления невидимых точек. В частности, такое применение координаты ^позволяет библиотека DirectX.
Для получения после проецирования значений 2Э, сохраняющих упорядоченность точек по расстоянию от наблюдателя, можно использовать следующее уравнение:
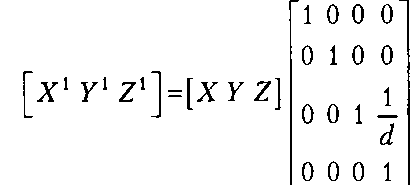
(24.9).В этом уравнении элемент Р44 матрицы проецирования Р2 равен единице. Его можно получить, совместив на рис. 24.3 плоскость проецирования с плоскостью ХУ мировой системы и поместив наблюдателя в точке Z = -с1. Тот же результат можно получить алгебраически, перемножив матрицы сдвига объектов мира вдоль оси Z на (I и проецирования Р,.
Данное уравнение эквивалентно следующей системе: Соответствующие выражения в декартовых координатах имеют следующий вид: Легко увидеть, что выражение (24.У) также задает операцию проецирования, но при совмещении проекционной плоскости с координатной плоскостью ХУ и помещении наблюдателя в точку (0, 0, -d) на оси Z. В качестве упражнения можно нарисовать соответствующую картинку и получить формулы проецирования из условия подобия треугольников.
В данном случае точки пространства, имеющие разные значения z, будут иметь и разные проекционные координаты z3. Поэтому, если две точки имеют одну проекцию, сравнение координат z.à позволяет отбросить дальнюю и рисовать ближнюю точку.
Координата z3 зависит от z нелинейно. По мере увеличения расстояния от наблюдателя при постоянном шаге в пространстве по оси z соответствующие точки 2Э будут располагаться все более близко, что может привести к ошибкам при выполнении теста глубины. Но если вероятность ошибки для удаленных объектов выше, чем для близких, то будет более эффективно использоваться ограниченная разрядность Z-буфера.
