[х\у] = [х,у]+[Сх,Су].
В соответствии с этим выражением, к каждой абсциссе прибавляется константа сдвига Сх, а к каждой ординате - константа сдвига Су.
Преобразования в однородных координатах
Перемножив матрицы поворота Р и масштабирования К, можно осуществить поворот и масштабирование всего лишь одной операцией умножения вектора на матрицу. Для объединения этих преобразований со сдвигом преобразования проводят в так называемых однородных координатах, которые получают при помощи ввода дополнительной координаты \¥. Точка (х} у) на плоскости в системе однородных координат описывается строкой /? = [X, У, Щ, где X = ]\?х, У = ]¥у. При №=\ однородные и декартовы координаты совпадают (X = х} У = у). В противном случае для перехода от однородных координат к декартовым нужно воспользоваться выражениями х = Х/]У, у= У/\У.
Непосредственной проверкой легко убедиться в том, что в однородных координатах все три преобразования представляются умножением вектора на матрицу размерности 3x3.
Преобразования на плоскости Сдвиг осуществляется следующей операцией:
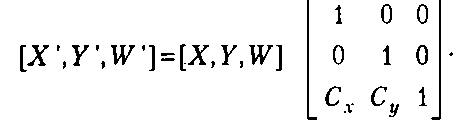
Поворот производится при помощи следующего преобразования:
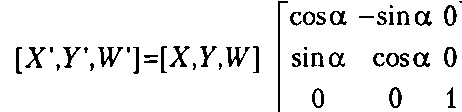
(24.1)Масштабирование осуществляется при помощи расчета следующего выраже ния:
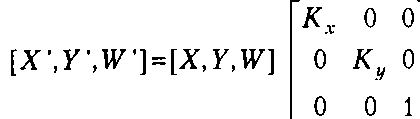
В данных преобразованиях \¥ = №\ поэтому удобно при переходе к однородным координатам дополнить координаты вершин (ху у) значением 1У= 1. Координаты точки при этом часто записывают в виде (х, г/, 1). Вводить отличное от единицы значение ]\? необходимо только при представлении матричной операцией проецирования точки на плоскость.
Использование однородных координат позволяет сократить объем вычислений, выполняемых при геометрических преобразованиях. Рассмотрим это на примере поворота треугольника ЛВС вокруг вершины г (рис. 24.1).
Предположим, координаты вершин имеют значения (8,7), (8,3), (6,3). Теперь нужно осуществить поворот треугольника по часовой стрелке на 90° (а = +90°). Это будет равносильно положительному (против часовой стрелки) повороту осей.
Так как выражение (24.1) описывает поворот вокруг начала координат, необходимо сначала преобразованием сдвига совместить вершину С с началом координат:
