В операционной системе Windows предусмотрено два варианта постановки и решения задач поворота, масштабирования и переноса изображений. Можно изменять уже сформированную в памяти картинку или предварительно задавать преобразования координат, которые потом будут применяться к каждой выводимой точке изображения.
Примеры реализации первого подхода уже рассматривались ранее. Функция BitBlt( ) переносит изображение, а функция StretchBlt( ) масштабирует его. Возможность вращения растрового изображения предоставляет функция ВЩ ), входящая в состав библиотеки DirectDraw.
Теперь необходимо рассмотреть методы, основанные на применении матрицы преобразования координат. Для осуществления поворота картинки необходимо повернуть вокруг заданного центра каждую ее точку. Данное преобразование можно рассматривать как поворот точки на заданный угол вокруг начала координат или как переход от описания объекта в системе координат XY к описанию в новой системе X'Y\ повернутой относительно XYна угол а.
Предположим, что точка А задана координатами (х, у) в системе XY. Теперь необходимо получить координаты (х',у') этой точки в новой системеX'Y\ оси которой повернуты на угол а относительно осей XY. Пусть радиус-вектор г точки А составляет угол ß с осью X. Тогда можно записать следующую систему уравнений: Преобразования на плоскости
X'=rcos (сс+ ß); Y'= г sin (cc + ß).
Геометрические преобразования
Раскрывая косинус и синус суммы двух углов, получим: х'= rcosP cosa - rsinPsina; у' = г cosP sina + г cosa sinP; Учитывая, что r cos = Р, а г sin Р - г/, получим окончательные выражения:
X'=xcosa-z/sina;
F'=xsina+z/cosa В матричной форме это будет выглядеть как R' = /?Р, где R = [дг, у], а /?' = [д:', г/ ].
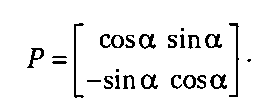
Если это же преобразование записать как умножение матрицы на столбец, то матрицу Р необходимо транспонировать.
Масштабирование объекта сводится к умножению соответствующих координат вершин на масштабные коэффициенты Кх, Ку, что в матричной форме можно записать следующим образом:
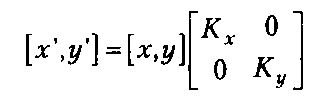
Сдвиг объекта можно представить следующим выражением:
