Основанию шестигранного куба соответствует проекция RGB куба вдоль его главной диагонали.
Ниже приводится программа для преобразования RGB в HSV и наоборот.
21 // File RGBHSV.cpp
void RGB2HSV (float r, float g, float b, float& h, f!oat& s, float& v)
{
float cMin = min3( r, g, b ); float cMax = max3( r, g, b ); float delta = cMax - cMin;
if (( v = cMax ) != 0 )
s = delta / cMax;
else
s = 0;
if ( s == 0 )
h = HUEJJNDEFINED;
else
{
jf(r==v)
h = (g-b)/delta;
else
if(g==v)
1. CBeT. LiBeTOBOCnpMflTMe. IjBeTOBbie MOflen
h = 2 + ( b - r) / delta;
else
h = 4 + (r-g)/delta;
if (( h *= 60 ) < 0 ) h += 360;
}
}
void HSV2RGB (float h, float s, float v, float& r, float& g, float& b )
{
, if ( s == 0 )
if (h == HUE_UNDEFINED ) r = g = b = v;
else
error ();
else {
if ( h == 360 ) h = 0;
h /= 60;
int i = floor ( h );
float f = h-i;
float p = v * (1 - s );
float q = v * (1 - s * f);
float t = v * (1 - s * (1 - f));
switch (i) {
case 0:
r = v;g = t;b = p; break;
case 1:
r = q; g = v; b = p; break;
case 2:
r = p; g = v; b = t; break;
case 3:
r = p; g = q; b = v; break;
case 4:
r = t; g = p; b = v; break;
case 5:
r = v; g = p; b = q; break;
}
}
}Компьютерная графика. Полигональные модели
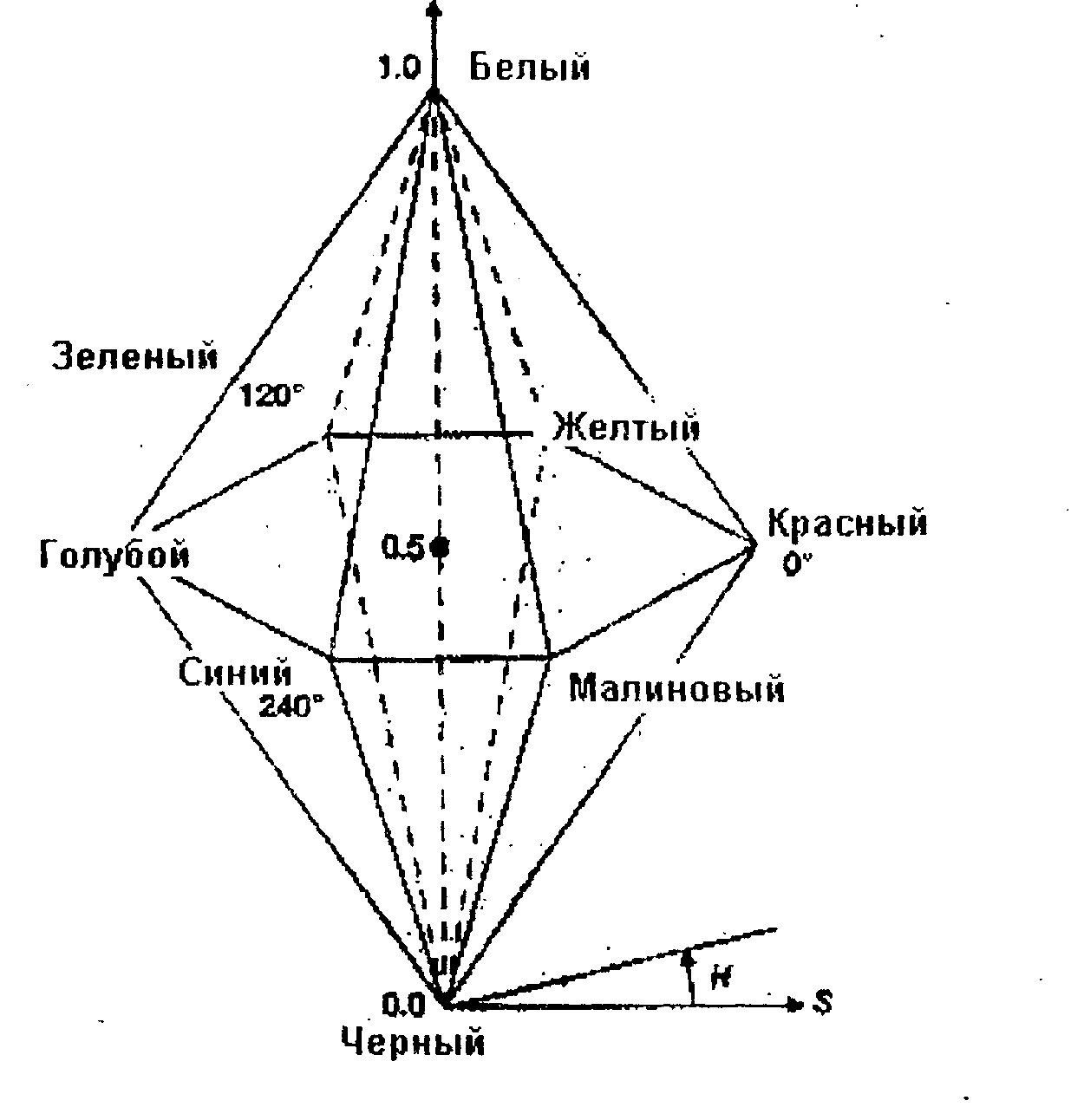
Еще одним примером системы, построенной на и нтуигив н ых поняти Я X тона, насыщенности и яркости, является система HLS (Hue, Lightness, Saturation). Здесь также используется цилиндрическая система координат, однако множество всех цветов представляет собой два шестигранных конуса, поставленных друг на друга (основание к основанию, рис. 1.10), причем вершина нижнего конуса совпадает с началом координат. Тон по-прежнему задается углом, отсчитываемым от вертикальной оси с красным цветом (угол 0°). Рис 1Ю
Порядок цветов на периметре общего основания конусов такой же, как и в моде ли HSV. Модель HLS можно рассматривать как модификацию модели HSV, где бе лый цвет сдвинут вверх, чтобы сформировать верхний конус из плоскости V- 1. Процедура для перевода цвета из модели HLS в модель RGB приводится ниже.
