Получающееся при этом изображение приведено на рис. 13.27.
Сразу бросается в глаза сильное искажение изображения вблизи линии, соединяющей противоположные вершины.
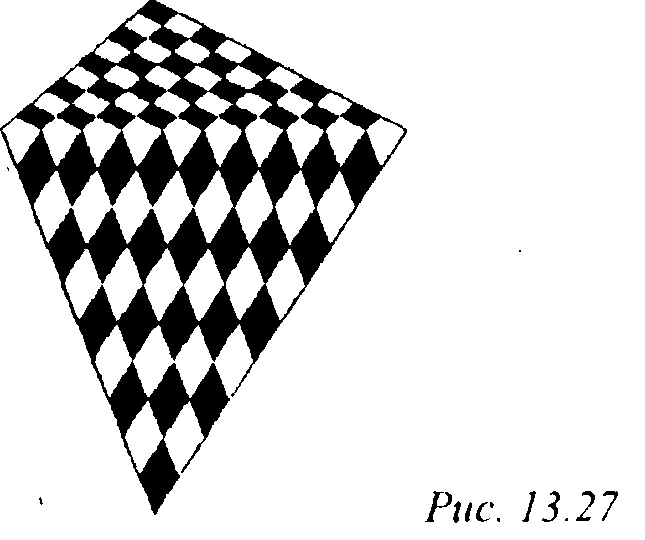
13. Элементы виртуальной реальности Это типичная ошибка закрашивания Гуро; отметим, что при интерполяции освещенности эти ошибки гораздо менее заметны, чем при интерполировании текстуры, так как интенсивность обычно является гладкой, медленно изменяющейся величиной, тогда как текстура часто имеет сильные скачки и разрывы. Наиболее сильно искажения заметны для текстур с ярко выраженной регулярной структурой.
Далее мы подробнее рассмотрим несколько интерполяционных методов в простейшем примере: построении горизонтальной строки пикселов, соответствующей некоторой грани (рис. 13.28).
Будем считать, что концам отрезка соответствуют столбцы *1 и х2 со значениями параметра текстурирования и! и и2 соответственно.
Простейшим вариантом является линейная интерполяция и(х) = Ъо + а\х,
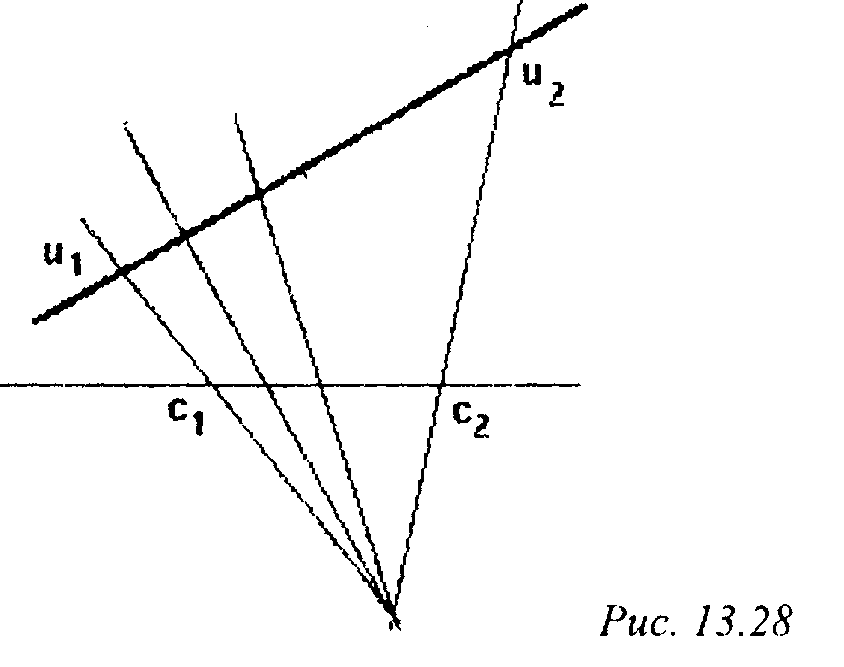
где значения параметров а$ и й\ легко определяются из соотношений и(х\) = и и, и(х2) - и2.
Несмотря на получающиеся при интерполяции ошибки, данный метод в целом ряде случаев оказывается вполне приемлемым.
Следующим возможным вариантом интерполяции является квадратичная: и(х) - ао + а\х + а2х .
Значение параметра щ обычно вычисляется, в некоторой промежуточной точке, Х1 4- Хп например в точке х^----.
Если точкам х\ и х2 соответствуют значения ,ЛМ1, Л2,&и2> то промежуточной точке л'з соответствует значение ит,--.
А] + Д2
Тогда значения параметров ао, а\ и а? находятся из соотношений
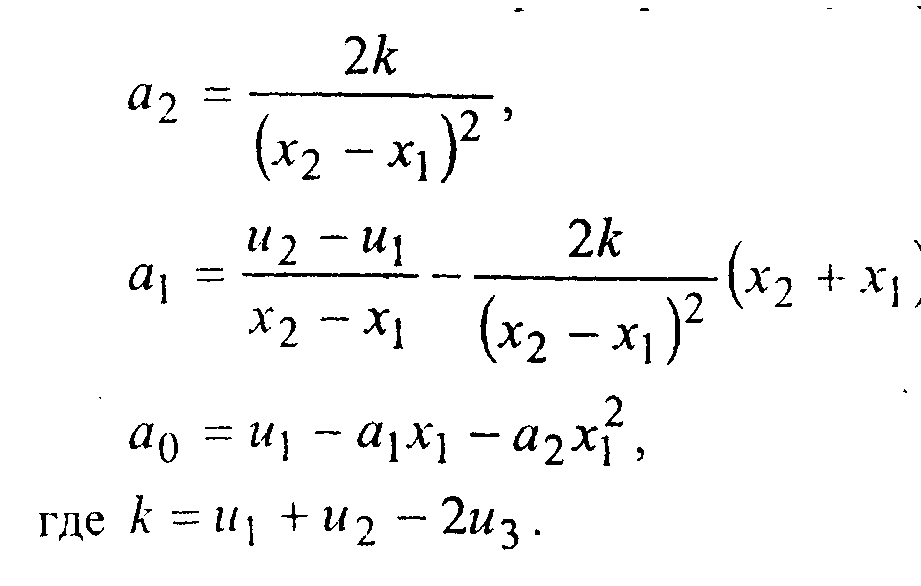
Компьютерная графика. Полигональные модели Поскольку нас интересует только набор значений и, то для облегчения расчетов можно произвести нормирование координат и считать, что х^ = О,ху = 1 их изменяется с шагом И. Тогда получаются заметно более простые уравнения для коэффициентов: а\ - -Зм| - г/2 + 4мз, ^2 = 2(wj + и2 - 2«з).
При этом для вычисления очередного значения и к операции умножения можно и не прибегать, достаточно воспользоваться рекуррентными соотношениями и(х\ + ih) = и(х\ + (/ - + d\, d\ =dj_} + 2a2h2, d$ = ajA + a2hxx.
