Это приводит к уравнению Хпх + Ynv + п- = const, т. е. каждая построенная группа пикселов является отрезком прямой картинной плоскости с нормалью (/7Х, пуу Несложно заметить, что все точки грани, проектирующиеся на этот отрезок, обладают одинаковой глубиной, т. е. являются пересечением грани с плоскостью, параллельной экрану.
В результате мы приходим к следующему алгоритму: проекция грани разбивается на набор параллельных отрезков с заданным угловым коэффициентом и но этим отрезкам рисуется.
Мы опять получаем минимум операций деления и умножения на пиксел, но за это приходится расплачиваться заметно более сложной схемой рисования.
Кроме того, в отличие от вертикальных и горизонтальных граней, когда перебирались пикселы, действительно лежащие на линии постоянства глубины, в данном случае перебираемые пикселы лежат на растровой развертке соответствующей линии, что приводит к заметным искажениям.
Описанный метод называется методом постоянной глубины (coflsta/zt-z).
Еще одним точным методом текстурирования является гиперболический метод. Запишем выражение для и в зависимости отх в пределах одной строки:
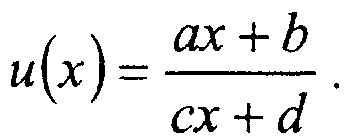
Правильное значение и удовлетворяет следующему уравнению: ] [х,и) = 0 , где /(х,и) = ах + Ъ - и(сх + а1).
Уравнение Дх, и) - О описывает гиперболу на плоскости переменных и и х. Поскольку величина х изменяется каждый раз на единицу, то для вычисления соответствующего значения и можно воспользоваться аналогом алгоритма Брезенхейма для построения гиперболы. Этот алгоритм обеспечивает достаточно высокое качество, но довольно сложен в реализации.
В ряде случаев прибегают к использованию интерполяционных текстур, когда вместо точных значений и и V для каждого пиксела экрана находятся их приближенные значения.
Существует довольно большое количество различных схем интерполяции, отличающихся как по затратам, так и по качеству получаемого изображения.
Простейшим вариантом интерполяции является билинейная интерполяция - аналог закрашивания Гуро, когда параметры текстуры сначала линейно интерполируются вдоль ребер, а затем - по горизонтальным линиям.
