Рассмотрим этот процесс подробнее.
Пусть игрок находится в точке (х*, у*) и угол между лучом и положительным направлением оси Ох равен а. Будем считать, что клетка, содержащая в себе игрока, имеет индекс а шаг сетки равен h.
Найдем точки пересечения луча с вертикальными линиями х = ih. Если направляющий вектор луча имеет положительную jc-составляющую (cos а > 0, т. е. -тс/2 < а < тс/2), то ближайшая точка будет иметь координаты
У\ -у + Ах tan а - у н- \jcj - jc Jtana
где Ах = h - (х* - i*h) - х\ - х* - расстояние вдоль оси Ох от положения игрока до ближайшей вертикальной линии справа.
При этом эта точка лежит на границе клетки
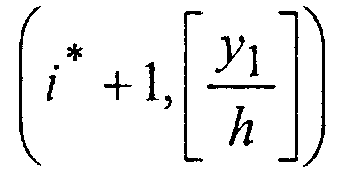
Если эта клетка занята стеной, то мы сразу получаем пересечение со стеной в точке (хь^). При этом расстояние до точки пересечения будет равно
_ Ах _ х\ - х
Если эта клетка пуста, то проверяем следующие точки: х,-+1 = х1- + И, Уи-1 "У* + ^ {та;
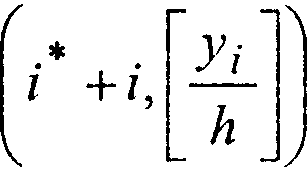
здесь i-я точка соответствует клетке проверка проводится до тех пор, пока мы либо не наткнемся на занятую клетку, либо не выйдем за пределы лабиринта.
Если клетка, соответствующая точке пересечения (х,;у,), занята, то расстояние до этой точки задается формулой
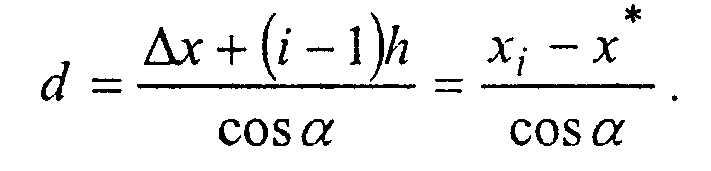
13. Элементы виртуальной реально Рассмотрим теперь случал, когда Л (к З/г^ cos а < 0, - <а<- .
U 2 )Ближайшая точка пересечения луча с линией вида х = Иг описывается формулами
X] = /* Л,
V; "V* - Ах tan а -у* + (*/ - х*) tan а; где Ах - х* - X].
( * \ у\ Г Первой проверяется клетка / - 1, -
I Lh \)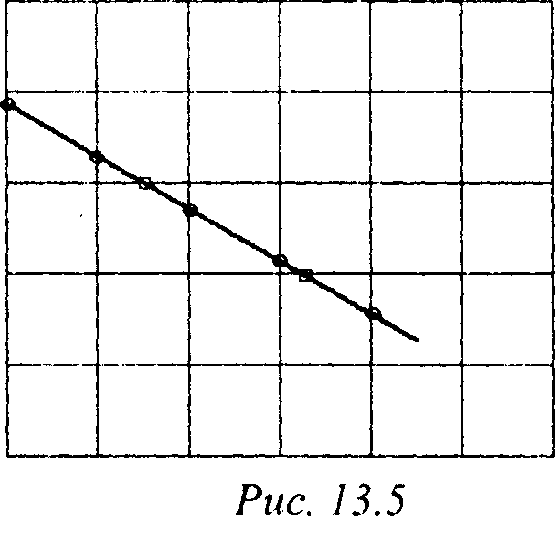
Если она занята, то пересечение найдено и расстояние до точки пересечения равно
*-Ах X] -х а--= --.
соэа соъа В противном случае необходимо проверить остальные точки пересечения:
*,-./= х,- - п, Ун 1==У1~ п tana; Для точки (х/, у,) следует проверить клетку
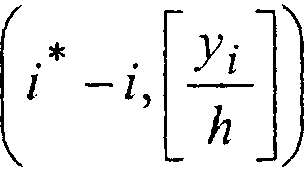
и в случае, если занята, расстояние до точки пересечения составит
^ _ Ах + (f -\)h xt - х*
-cos a cos а В результате мы приходим к следующему алгоритму:
float checkVWalls (float angle )
{
int xTile = (int) locX; // cell indices int yTile = (int) locY; float xlntercept; // intercept point