Тем самым следующая линия будет рисоваться только в тех местах, где ее проекция лежит вне области, задаваемой контурными линиями (рис. 10.9).

10. Удаление невидимых линий и поверхностей Пусть проекцией линии z = J{x, у к) на картинную плоскость является линия У -Yk(X), где (X, Y) - координаты на картинной плоскости, причем У - вертикальная координата. Контурные линии Y^max{X) и Y^nijn(X) определяются следующими соотношениями:
, YLx(X)= max Yj(X),l<i<k-l У^П(Х)= min Yj(X).
min l<i<k-lНа экране рисуются только те части линии У =? Yk(X), которые находятся выше линии Ykmclx(X) или ниже линии Ykmin(X).
Такой алгоритм называется методом плавающего горизонта.
Возможны разные способы представления линий горизонта, но одной из наиболее простых и эффективных реализаций данного метода является растровая реализация, при которой каждая линия горизонта представлена набором значений У с шагом в 1 пиксел.
int YMax [SCREEN_WIDTH];
int YMin [SCREEN_WIDTH];Для рисования сегментов этой ломаной используется модифицированный алгоритм Брезенхейма, который перед выводом очередного пиксела сравнивает его ординату с верхней и нижней контурными линиями.
Замечание. Случай отрезков с угловым коэффициентом по модулю, большему единицы, требует специальной обработки (чтобы не появлялись выпадающие пикселы (рис. 10.10)).
Реализация этого алгоритма приведена ниже.
21 // File examplel .срр #include <conio.h> #include <graphics.h> #include <math.h> #include <process.h> #include <stdio.h> #include <stdlib.h>
#define NO_VAlUE 7777
struct Point // screen point
{
int x, y;
};
int YMax[640];
int YMin[640];
int upColor = LIGHTGREEN;
int downColor = LIGHTGRAY;
void drawLine ( Point& p1, Point& p2 )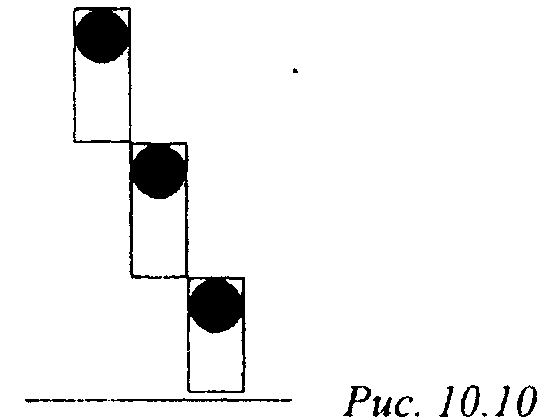
Компьютерная графика. Полигональные модели
\п\ ах = аЬэ ( р2.х - р1.х ); Ы бу = аЬв ( р2.у - р1 .у ); бх = р2.х >= р1.х ? 1 : -1; \п\ ву = р2.у >= р1.у ? 1 : -1;
\1 ( бу <= бх ) {
\п\ б = -ах; Ы 61 = бу « 1;
|"п1 62 - ( ау- с1х ) « 1;
