Рассмотрим сначала построение графика функции в виде набора линий, соответствующих постоянным значениям у, считая, что углы (р и у/ подобраны таким образом, что при>>1 > у2 плоскость у = у\ расположена ближе к картинной плоскости, чем плоскость у = у2.
Программу, осуществляющую построение графика функции двух переменных без удаления невидимых линии, написать несложно, однако получающееся при этом изображение зачастую оказывается слишком запутанным и непонятным (рис. 10.6). Поэтому естественным образом возникает задача о таком способе построения графика функции двух переменных, при котором невидимые линии удалялись бы (рис. 10.7).
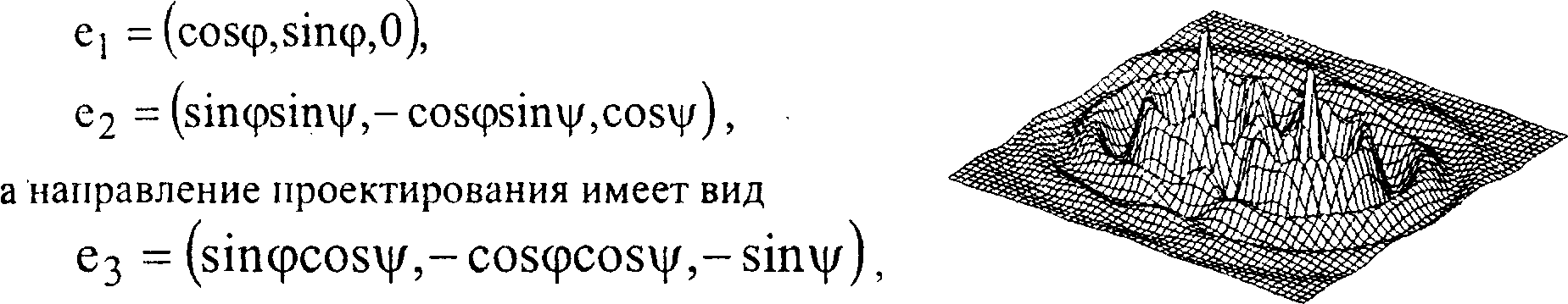
Рис. 10.5
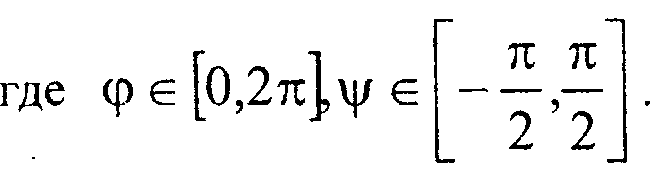
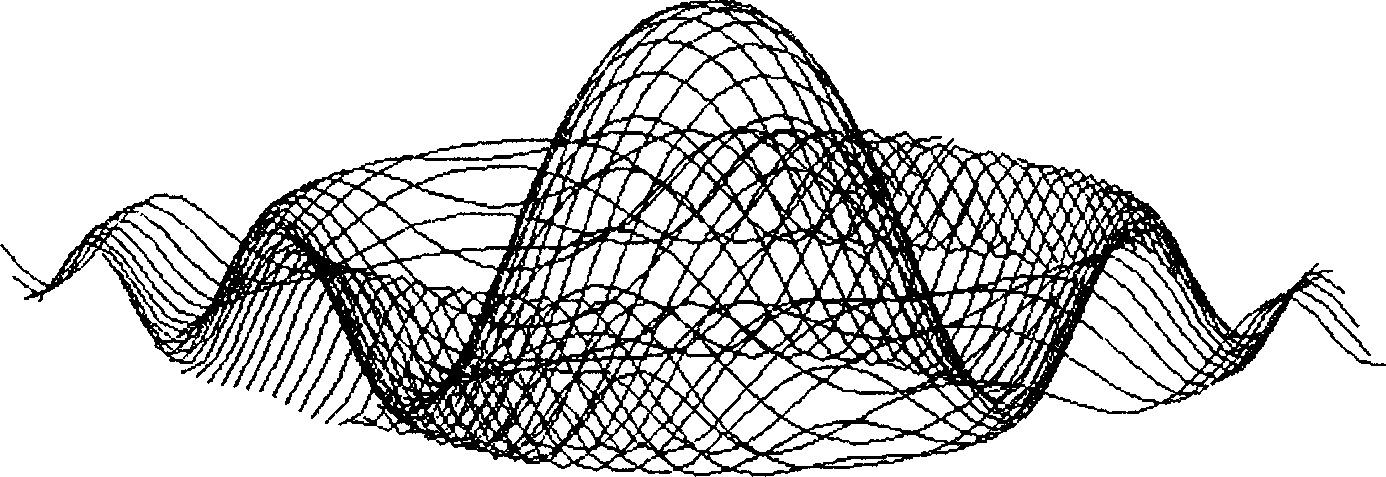
Рис. 10.6
Компьютерная графика.. Полигональные модели

Каждая линия семейства z = fix, Vj) лежит в своей плоскости у = у„ причем все эти плоскости параллельны и, следовательно, не могут пересекаться. Из этого следует, что при V/ > у, линия z = f(x, yj) не может закрывать собой линию z = f(x, yj и, значит, каждая линия z = f(x, у/) может быть закрыта только предыдущими линиями
z =f(x,yd, ' = Ь …,У-1.
Тем самым возможен следующий алгоритм построения графика функции z = f(x, у)"images/tmp32A8-145.png" alt="Рассмотрим область экрана между верхней и нижней линиями горизонта - она является проекцией части графика функции, заключенной в полосе у; <у <у2, и, очевидно, находится ближе, чем все остальные линии вида z =/{х, у,), / > 2. Поэтому те части линий, которые при проектировании попадают в эту область, указанной частью графика закрываются и при данном способе проектирования не видны.">
Рис. 10.8
Рассмотрим область экрана между верхней и нижней линиями горизонта - она является проекцией части графика функции, заключенной в полосе у; <у <у2, и, очевидно, находится ближе, чем все остальные линии вида z =/{х, у,), / > 2. Поэтому те части линий, которые при проектировании попадают в эту область, указанной частью графика закрываются и при данном способе проектирования не видны.
