Пример 1. Построить матрицу вращения на угол <р вокруг прямой Ь, проходящей через точку А(а, Ъ, с) и имеющую направляющий вектор (I, т, п). Можно считать, что направляющий вектор прямой является единичным: Компьютерная графика. Полигональные модели
1 2 2 *I + т + п = 1.
На рис. 9.1 схематично показано, матрицу какого преобразования требуется найти.
Решение сформулированной задачи разбивается на несколько шагов. Опишем последовательно каждый из них.
1-й шаг. Перенос на вектор -А(-а, -Ь, -с) при помощи матрицы
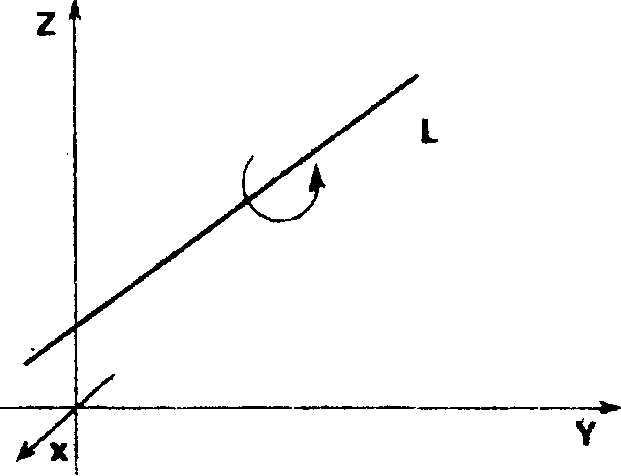
Рис. 9. і
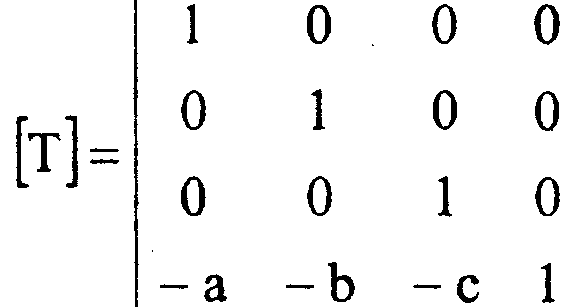
В результате этого переноса мы добиваемся того, чтобы прямая Ь проходила через начало координат.
2-й шаг. Совмещение оси аппликат с прямой Ь двумя поворотами вокруг оси абсцисс и оси ординат.
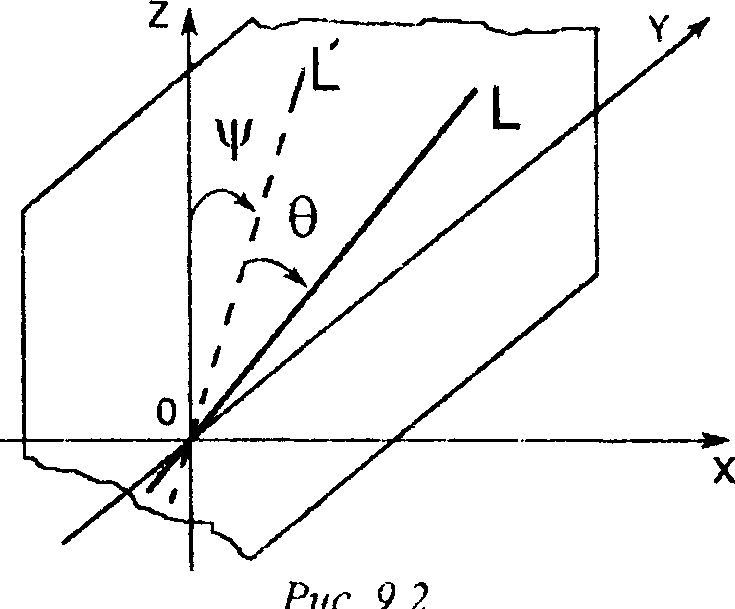
Первый поворот - вокруг оси абсцисс на угол у (подлежащий определению). Чтобы найти этот угол, рассмотрим ортогональную проекцию V исходной прямой Ь на плоскость X -0 (рис. 9.2).
Направляющий вектор прямой V определяется просто - он равен (0, т, л). Отсюда сразу же вытекает, что п т соз\|/ - - , злп у = - ,
Соответствующая матрица вращения имеет следующий вид"images/tmp32A8-98.png">
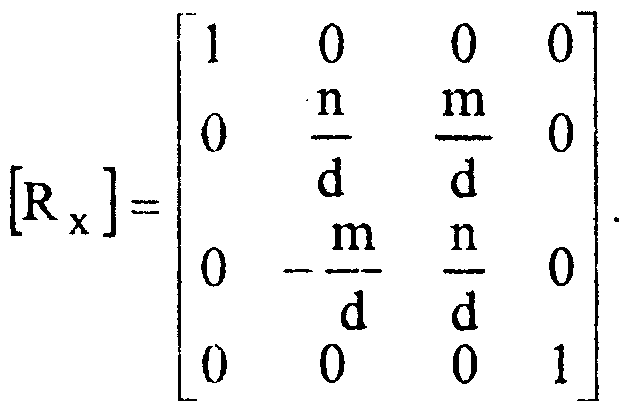
Под действием преобразования, описываемого этой матрицей, координаты вектора (/, /7?, п) изменятся. Подсчитав их, в результате получим
9. Преобразования в пространстве, проектирование
(/,1я,и,1)[^]= (/,0,^,1).
Второй поворот - вокруг оси ординат на угол 0, определяемый соотношениями соб# = 1,ът в - -а1. *
Соответствующая матрица вращения записывается в следующем виде:
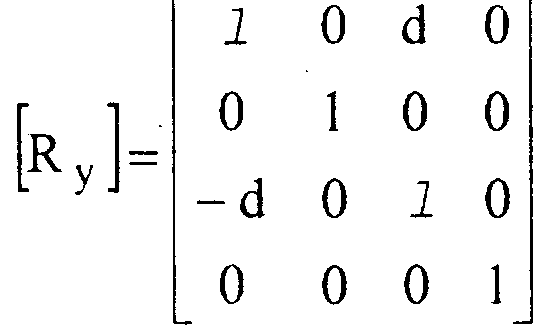
3-й шаг. Вращение вокруг прямой Ь на заданный угол <р, Так как теперь прямая Ь совпадает с осью аппликат, то соответствующая матрица имеет следующий вид:
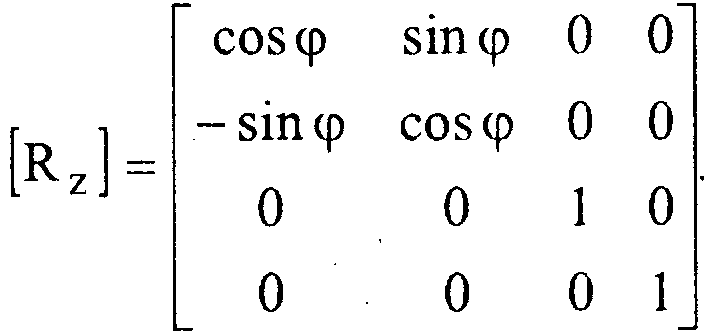
4- й шаг. Поворот вокруг оси ординат на угол -В.
5- й шаг. Поворот вокруг оси абсцисс на угол -у.
Замечание. Вращение в пространстве некоммутативно. Поэтому порядок, в котором проводятся вращения, является весьма существенным.
6- й шаг. Перенос на вектор А(а, Ъ, с).
Перемножив найденные матрицы в порядке их построения, получим следующую матрицу: Выпишем окончательный результат, считая для простоты, что ось вращения Ь проходит через начальную точку:
