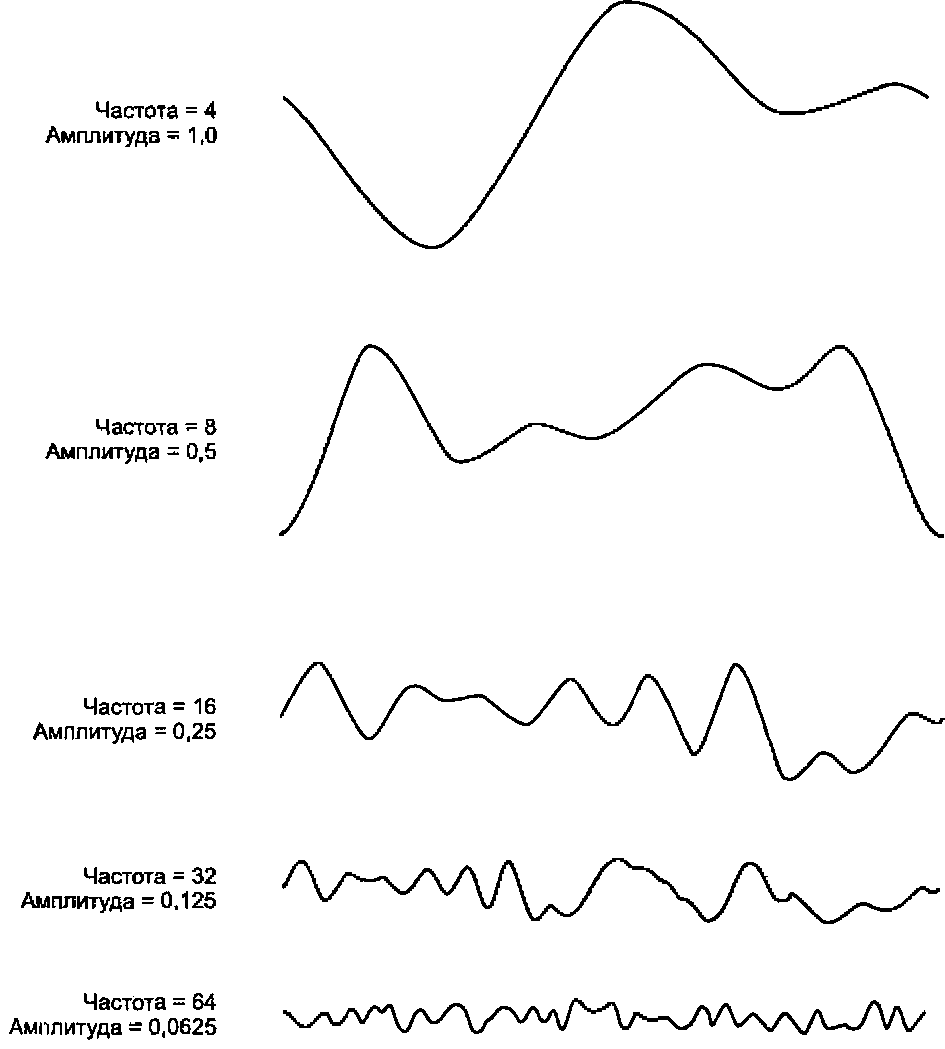
Рис. 12.3. Изменение частоты и амплитуды функции шума Как можно видеть на рисунке, с увеличением частоты и уменьшением амплитуды «помехи» становятся мельче. Отношение двух частот друг к другу в масштабе 2"images/tmp16FC-37.png" alt="Результат сложения функций шума различной частоты и амплитуды">
Рис. 12.4. Результат сложения функций шума различной частоты и амплитуды
В результате получается функция, которая содержит «помехи» различных размеров. Большие выпуклости на низкочастотных функциях обеспечивают общую форму, а меньшие выпуклости на высокочастотных - детализацию, заметную при уменьшении масштаба. Перлин назвал функцию суммы последовательных октав с разницей в половину амплитуды функцией шума 1//, но сейчас более популярно другое название - «отрывочное броуновское движение» («fractional Brownian motion», или «ffim»).
12.1. Определение шума Если различные октавы шума суммируются в процедурном шейдере, наступает момент, когда некоторые частоты могут вызвать нежелательные дефекты изображения. Алгоритмы, учитывающие необходимость сглаживания функций шума, обычно прекращают наложение октав раньше, чем частота станет настолько высокой, чтобы вызвать дефекты. Вместо этого можно сделать функцию более плавной в месте, где появляется Дефект.
Функцию шума, разработанную Перлином (шум Перлина), иногда называют градиентным шумом. Она определена как функция со значением 0 для каждого целого входного значения; для каждой из этих точек определяется псевдослучайный градиентный вектор. Характеристики этой функции шума позволяют использовать ее для некоторых эффектов [2]. Именно эта функция используется sRenderMan как функция шума, и она же, скорее всего, будет использоваться в реализациях встроенной функции noise языка шейдеров OpenGL.
