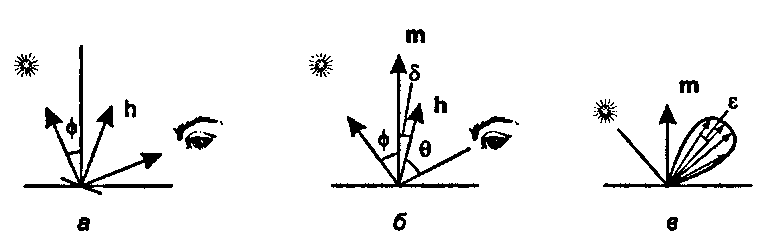
Рис. 14.18. Определение доли микрограней, ориентированных под утлом 5
Были разработаны различные виды функций распределения. Кук и Торренс использовали распределение Бекмана [Beckmann, 16], описываемое формулой для плотности"images/tmp8E4A-906.png">
(14.25)которое дает хорошее математическое приближение для многих имеющихся шероховатых поверхностей. Это распределение имеет максимум при б - 0 и быстро уменьшается при возрастании б. Параметр т определяет степень шероховатости поверхности. (Он является среднеквадратическим наклоном микрограней.) Величина этого параметра варьируется от значения 0,2 для почти гладких поверхностей до 0,6 для шероховатых. При малых значениях т плотность распределения .0(8) быстрее убывает с ростом б.
Кук и Торренс включили распределение .0(6) в качестве масштабного множителя зеркальной составляющей отражения в различных направлениях, а за б приняли угол между векторами пит. На рис. 14.18, в показано изменение интенсивности зеркального отражения для различных направлений наблюдения при т - 0,3. Этот рисунок похож на «диаграмму излучения» с рис. 8.12. Относительной величине зеркальной составляющей в каждом направлении соответствует длина стрелки. Она является наибольшей в направлении полного отражения (под углом ф), поскольку нормали микрограней чаще всего параллельны вектору т. При отклонении от направления полного отражения, скажем на
14.7. Рисование закрашенных изображений сцен угол е, эта величина уменьшается, так как при этом микрогрань должна иметь нормаль, направленную на е/2 в сторону от т, а из плотности распределения следует, что таких граней меньше (см. упражнения в конце раздела).
Затенение и экранирование Торренс и Спэрроу учитывали также эффекты «экранирования» («masking») и «затенения», которые могут иметь место на поверхности, состоящей из микрограней. Это привело к появлению «геометрического члена» G, масштабирующего интенсивность зеркальной составляющей. На рис. 14.19 показана зависимость этого эффекта от геометрии типичной грани. На рис. 14.19, а луч падает на грань под таким углом, что вся грань освещена и весь свет «уходит» с грани. В этом случае коэффициент G будет равен единице. На рис. 14.19, б направление отражения относительно вектора h таково, что часть света, покидающего грань, экранируется ребром соседней грани. Для учета этого эффекта значение G соответственно уменьшается. На рис. 14.19, в освещена только часть грани, а остальная ее часть затенена ребром соседней грани. В этом случае коэффициент G меньше единицы.
