Г-'(5 + сг) = (Г-'S) + (Г-'с) г.
На рис. 14.6 этот луч обозначен 5' + c't. Неудивительно, что обратно преобразованный луч является по-прежнему лучом, то есть прямой линией, выходящей из точки S' в направлении с'. Предположим, что преобразованию Т соответствует матрица М. Тогда, используя однородные координаты, получим следующее уравнение для обратно преобразованного луча:
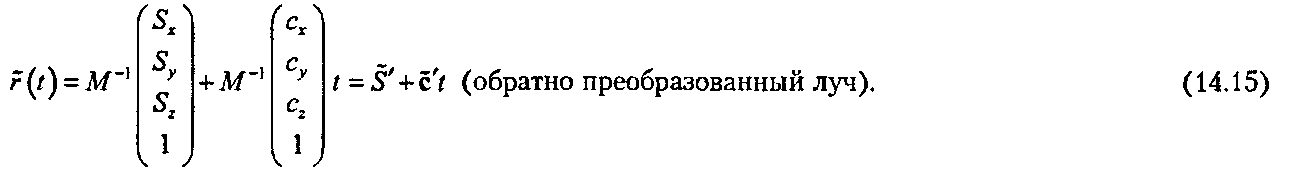
Отметим, что матрица М~[ в одном случае умножается на точку, а в другом случае - на вектор. 5' формируется из S' путем отбрасывания 1; а с' формируется из с' отбрасыванием 0.
Таким образом, вместо попыток определить пересечение луча с преобразованным объектом, мы исследуем пересечение «обратно преобразованного» луча с базовым объектом. Применяется описанная ниже технология.
Каждый объект в списке объектов обладает своим собственным аффинным преобразованием. Для пересечения луча S + et с преобразованным объектом мы: О Обратно преобразуем луч (получаем S' + c't). О Находим время соударения th этого луча с базовым объектом.
О Используем это же время th в луче S+ et для нахождения фактической точки соударения.
Изящество данного подхода заключается в том, что нам требуется разработать код, относящийся только к пересечению луча с базовым объектом. Это вдвойне выигрышная ситуация (выигрывает программист и выигрывает компьютер): мы можем применять к объектам аффинные преобразования для целей моделирования (чтобы получить нужные нам сцены) и не платим за это усложнением кода подпрограмм, вычисляющих пересечение. «Расходы на аффинное преобразование» просто перекладываются на преобразование самого луча.
Пример 14.4.3. Где заданный луч соударяется с преобразованной сферой?
Предположим, что эллипсоид информируется из базовой сферы при помощи следующих SDL-команд:
translate 2 4 9 scale 14 4 sphereТо есть базовая сфера вначале масштабируется и затем сдвигается. Прямое и обратное преобразования этой сферы соответственно имеют следующие матрицы:
Введение в трассировку лучей
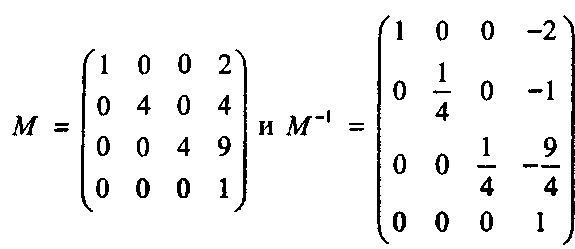
(Проверьте их!) Определите, где луч (10,20,5) + (-8, -12,4) г пересекается с W. Решение
