S + ett - (3,2,3) (1 - 0,7868) - (0,6393, 0,4264,0,6396); S + ct2 - (3,2,3) (1 - 1,2132) - (-0,6393, -0,4264, -0,6396).Легко заметить, что обе эти точки находятся на единичном расстоянии от начала координат, как и следовало ожидать. Обратите внимание на красивую симметричность точек соударения; она возникает здесь в силу того, что луч проходит через начало координат и центр базовой сферы тоже располагается в начале координат.
14.4.3. Пересечение луча с преобразованными объектами Если я пытаюсь объяснить спрашивающему меня, что это означает, то я не знаю.
Св. Августин о природе времени С каждым объектом сцены связано преобразование Т, придающее ему желаемые размер, ориентацию и положение на сцене. А что это преобразование делает с уравнениями и результатами, полученными нами в предыдущем разделе?
Эта задача иллюстрируется рис. 14.6: преобразование Т отображает базовую сферу W в эллипсоид W. Спрашивается: когда луч S + ct пересечется с W? Допустим, что может быть найдена неявная форма G( ) для преобразованного объекта W. Тогда для определения времени соударения требуется решить уравнение G(S + et) - 0.
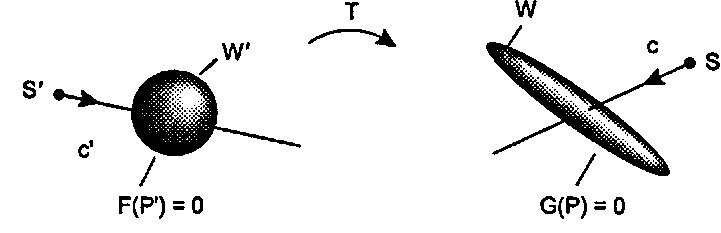
Рис. 14.6. Пересечение луча с эллипсоидом
14.4. Пересечение луча с объектом Таким образом, задача сводится к нахождению неявной формы преобразованного объекта. Однако из раздела «Влияние аффинного преобразования» главы 6 мы знаем, что если неявная функция исходного базового объекта равна £(Р), то для преобразованного объекта она приобретает вид Р(Т~1(Р)), где Г"1 - преобразование, обратное Г (то есть матрица преобразования Т'1 равна М"1, если преобразованию Г соответствует матрица М). Таким образом, нам нужно решить следующее уравнение"images/tmp8E4A-889.png">
(14.14)относительно времени соударения t. Это уравнение может оказаться весьма неприятным. Однако в действительности оно просто означает решение для времени, при котором обратно преобразованный луч (inverse transformed ray) T~i(S+ ct) соударяется с исходным базовым объектом! Поскольку преобразование Г линейно, обратно преобразованный луч можно представить в виде:
