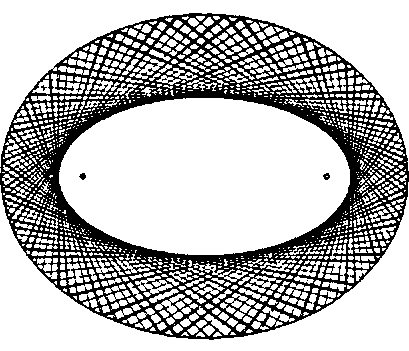
Рис. 11.63. Лучи, касательные ко второму эллипсу
О Если луч при первом прохождении проходит между фокусами, он будет описывать бесконечную траекторию, которая никогда не приблизится к фокусам больше, чем гипербола с теми же фокусами, как показано на рис. 11.64. Напишите программу, имитирующую эллиптипул, и поупражняйтесь с ней. Пользователь каким-либо способом задает начальное положение и направление луча, после чего траектория луча прослеживается на протяжении большого числа отражений. Пусть пользователь задает и способ прохождения луча относительно фокуса. (Имейте в виду, что в этом случае ошибки округления могут привести к непредсказуемым эффектам. Как можно нейтрализовать действие такой ошибки?) Пусть луч изменяет
Создание кривых и поверхностей
свой цвет таким образом, чтобы текущая траектория луча выделялась на фоне заполнения экрана старыми траекториями. Поэкспериментируйте с эллипсами, имеющими различные эксцентриситеты, включая круглые столы для пула.
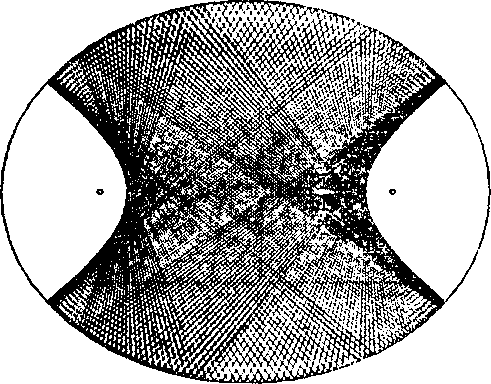
Рис 11.64. Лучи, касательные к гиперболе Дополнительное задание. Расширьте условия эксперимента и поместите внутрь стола препятствия круглой или другой формы (например, эллиптической). Составят ли в этом случае траектории лучей какой-нибудь известный узор?
Дополнительное задание. Повторите эксперимент, задав в качестве формы стола суперэллипс. Подумайте, как вычислить соударения луча и стены, а также внутреннюю нормаль к стене в любой ее точке.
Тематическое задание 11.3. Кривые Безье Уровень сложности П.
Напишите программу, которая принимает последовательность контрольных точек, вводимую пользователем с помощью мыши, и рисует на базе этих точек кривую Безье. Точки на кривой вычисляются для близких значений t и соединяются прямолинейными отрезками. Выполните свою программу при различных количествах контрольных точек. Обратите внимание на замедление вычислений при большом числе контрольных точек, поскольку в этом случае степень полиномов возрастает.
Тематическое задание 11.4. Генератор квадратичной сплайн-кривой Уровень сложности II.
