которое является квадратным относительно и Квадратные уравнения легко поддаются решению и имеют нуль, одно или два решения, что соответствует для нас следующим событиям.

О Нет решений: луч минует эллипс.

О Одно решение: луч касается эллипса.

О Два решения: луч входит в эллипс и затем выходит из него.

Если начало луча лежит внутри камеры, то одно из решений положительное, а другое отрицательное (почему?) Возьмем положительное решение и назовем его Требуется найти направление отраженного луча в точке соударения. Образуем из выражений уравнения (11.3) х(£) = асоэ(г) и г/(£) = &зт(г) нормальный вектор (-&соз(г), -азт(£)), что в терминах х и у выглядит как {-Ьх/а, -ау/Ъ). Поскольку нам нужно только направление нормали, то удобнее изменить масштаб и представить формулу в виде

y(t) - sin(2nM),
(11.98)

Тематическое задание 11.2. «Эллиптипул»

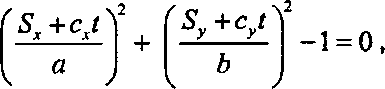
1 Пул (pool) - род игры в бильярд. - Примеч. пер.

11.13. Тематические задания

(-Ь2х, -а2у). Нам требуется внутренняя нормаль, так как луч отражается от внутренней стенки эллипса. Рассматривая рис. 11.62, можно увидеть, что х- и ^-компоненты внутренней нормали отрицательны при положительных х и у, поэтому именно выражение п - (-Ь2х, -а2у) (11.99)

является направлением внутренней нормали. Направление отраженного луча г можно определить подстановкой уравнения (11.99) в уравнение (4.27).

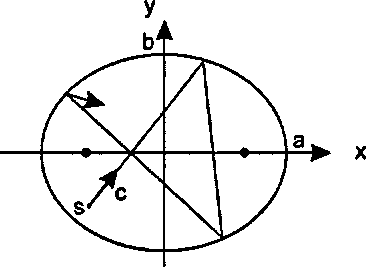
Рис. 11.62. Имитация эллиптипула Имитация эллиптипула демонстрирует некоторые особенности его поведения"opengl1_831.html">⇐ Предыдущая| |Следующая ⇒