Уровень сложности II.

Обобщение эллипса. В параметрическом представлении эллипса фигурирует один синус и один косинус. Можно сформировать интересное семейство кривых, если наложить несколько эллипсов, которые пробегаются с различными скоростями. Такое «суммирование гармоник» напоминает графики рядов Фурье, которые встречались нам в главе 3, однако теперь это осуществляется сразу в двух измерениях. Начнем с двух членов, а потом обобщим. Рассмотрим семейство кривых, описываемое уравнением:

x(t) = Xtcos(2nt) + X2cos(2nkt);
y(t) = y,sin(2n£) + Y2sin(2nkt). (11.95)

Первый член в каждой формуле представляет собой эллипс, к которому добавлен второй дополнительный («piggyback») эллипс, пробегающий свою траекторию в k раз быстрее. При изменении t от О до 1 первый эллипс пробегается один раз, в то время как второй - k раз. Если k - целое, то фигура будет в точности замкнутой. Напишите программу, рисующую такие периодические фигуры по вводимым в нее значениям Xv Х2, У,, Х2, к Обобщите задачу, добавив в x(t) и y(t) больше членов.

Огибающая окружности. Отметим точку Р на куске нити, намотанной на ручку швабры. Держа ленту натянутой, размотаем ее, поворачивая ручку швабры рукой. Траектория, которую опишет точка Р, - это спираль, известная как «огибающая окружности». Нить, соединяющая окружность (ручку швабры) с точкой Р, является касательной к окружности. Очевидно, что эта касательная всегда перпендикулярна к спирали. Кроме того, последовательные витки спирали параллельны друг другу и отстоят друг от друга на одно и то же расстояние. (Чему равно это расстояние?) Семейство таких спиралей формируется путем вращения фигуры (или выбором различных точек Р на нити). Каждая спираль ортогональна ко всем прямым, касательным к окружности. Параметрическая форма этой кривой имеет вид:

x(t) = cos(2nr) + 2nts'm(2nt);

y(r) = sin(2nt) - 2ntcos(2nt)- (11.96) Напишите программу, которая рисует огибающие окружности.

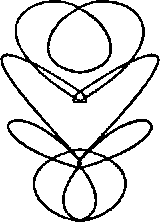
Рис. 11.61. Взлетающий джинн Другие синусоидальные кривые. Небольшие изменения в выражениях для x(t) и y(t) из предыдущего упражнения могут привести к сильно различающимся формам. Например, кривая, изображенная на рис.11.61 (разработанная профессором Робертом Везером (Robert Weaver) из колледжа Mount Holyoke, South Hadley, Massachusetts), получена из следующих функций"opengl1_829.html">⇐ Предыдущая| |Следующая ⇒