О Первые производные в концевых точках Р0 и PL равны нулю.
О Третьи производные в точках Р, и Р£_, непрерывны. (Это называется «безузловым» условием Бура (Boor's «not-a-knot» constraint); в результате два первых сегмента становятся одним полиномом; то же относится и к последним сегментам.)
О К концам контрольного полигона добавляются две «ложные» точки (подойдут, например, Р , и PL). Кривая по-прежнему рисуется от точки Р0 до точки Рг однако теперь в этих двух точках можно вывести выражения для скоростей.
11.10.7. Прохождение параболы через контрольные точки Для нахождения наклона в точке Рк можно найти единственную параболу, проходящую через три точки Рк_Рк, Рк+и вычислить ее скорость в точке Рк (рис. 11.49). Найдите формулу для этой скорости по любым трем контрольным точкам.
Создание кривых и поверхностей
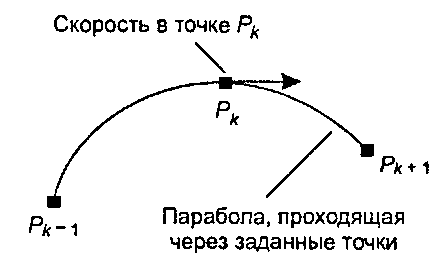
Рис. 11.49. Задание скорости с помощью параболы, проходящей через три точки
11.10.5. Интерактивное задание касательных векторов В некоторых программах рисования (САСБ) дизайнеру предлагаются видимые «рукоятки» для задания касательных векторов, как показано на рис. 11.50. Пользователь размещает контрольные точки, после чего рисуется первоначальная интерполирующая кривая. Затем пользователь с помощью мыши перемещает различные рукоятки, в результате чего соответствующие касательные векторы изменяются, а новая кривая непрерывно замещает старую. Такая видимая обратная связь позволяет пользователю быстро отредактировать кривую до желаемой формы.
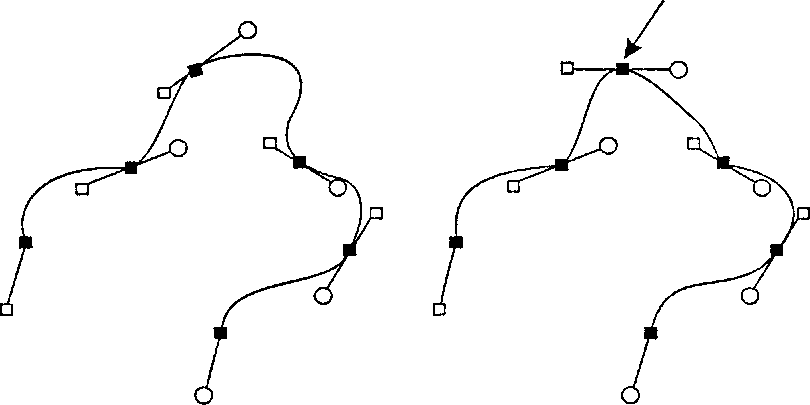
а б Рис. 11.50. Интерактивное задание кубических сегментов
11.11. Моделирование криволинейных поверхностей До сих пор мы занимались вопросами представления и генерирования кривых в дву- и трехмерном пространстве. Естественно распространить эти идеи на создание криволинейных поверхностей. В главе 6 нами было рассмотрено множество поверхностей различных типов, таких как линейчатые поверхности, билинейные лоскуты и лоскуты Кунса, а также поверхности вращения. Рассмотрим теперь применение для создания этих поверхностей кривых Безье и В-сплайнов и таким образом разработаем мощные инструменты для создания обширного множества криволинейных поверхностей.
