при с - 0 ск - х4, прис=1 Зак + 2Ьк + ск = зк+1.
Эти два уравнения содержат еще 2Ь условий, поэтому всего мы имеем 4Ь условий для 41 неизвестных коэффициентов. Отметим, что из требования равенства производных заданным значениям наклона автоматически вытекает непрерывность наклона в узлах, поэтому кривая 1-гладкая.
Исходя из этих уравнений, нетрудно аналитически выразить искомые коэффициенты через ук и «4. (Проверьте это.) Итак, для к - О,1.....Ь - 1 мы имеем:
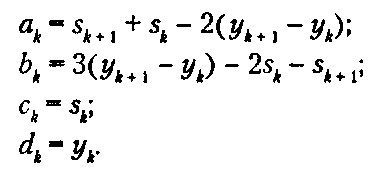
Эти уравнения определяют компоненты ук(£) для каждого сегмента. Аналогично могут быть получены уравнения, определяющие коэффициенты хк(€), после чего можно нарисовать эти кубические сегменты уже известным способом, вследствие чего будет сформирована кусочная кубическая кривая.
Решение можно было бы считать законченным, если бы мы знали значения наклонов $к для каждого ук. Существует несколько методов определения этих значений. Посмотрим вначале, какое влияние оказывает наклон «4 на форму кривой. Затем посмотрим, как сделать кривую 2-гладкой. Это приведет нас к «естественному» кубическому сплайну.
Пример 11.10.1.0 касательных и наклонах
С целью лучшего понимания соответствия только что рассмотренных нами многочисленных коэффициентов друг другу, рассмотрим кривую, состоящую из двух кубических сегментов, Я0(г) и /?,(?). со следующими свойствами: Сегмент 0. /?0(?) проходит через точку (1, 1) при г - 0 и через точку (4, 3) при г - 1. Кроме того, его скорость равна (1,0) при г - 0 и (0,5) при г = 1, где 5 - некоторая величина, которую мы будем варьировать для выяснения зависимости от изменений наклона кривых.
Сегмент 1. /?,(?) проходит через точку (4,3) при г - 0 и через точку (0,3) при г - 1. Скорость равна (0,5) при г - 0 и (0,1) при г - 1. Результирующая кривая для частного случая 5=1 приведена на рис. 11.41. Параметрические сегменты показаны в плоскости ху; кроме того, на рисунке изображены компоненты *0(г), *,(*)> Уа(0> У.(0< образующие данную кривую.
Внимательно проследим за ходом кривой и обратим внимание, как образуется ее форма из форм отдельных составляющих. Заметим, что кривая плавно переходит от одного сегмента к следующему, поскольку ее скорость в этих точках непрерывна. Это обеспечивается непрерывностью на стыке функ-
