for (к - 0: к < L: к++) {

retrieve the coefficients А[к]. В[к]. С[к]. D[k] // вычисляем коэффициенты А[к]. В[к]. С[к]. D[k]

Draw the curve Rk(t). using these coefficients

in short line segments, as t goes from 0 to 1 // рисуем кривую Rk(t) по этим коэффициентам // короткими сегментами линий при изменении t от 0 до 1 }

Сегмент Rk(f) - (x(t), y(t)) является, как всегда, 2Б-кривой. Если функция R(t) интерполирует точку Р = (х, у), то функции x(t) и y(t) должны интерполировать компоненты этой точки - соответственно X и у. Поэтому можно рассматривать процесс интерполяции раздельно для компонентов х и у. Это упрощает обозначения и, кроме того, облегчает наблюдение того, что происходит.

На рис. 11.40, а показана задача интерполяции только для ^-компонента. Задана последовательность значений у: (у0, yv…, yL); требуется найти такой кусочный кубический полином, который проходил бы через эти значения у и обладал 1-гладкостью. (В некоторых случаях мы сделаем этот полином даже 2-гладким, то есть сплайном), *-й кубический сегмент кривой, показанный на рис. 11.40, б, описывается следующей формулой:

yk(t) - akt3 + bkt2 + ckt + dk, где* - 0,1.....L - 1; для г в промежутке [0,1]. (11.75)

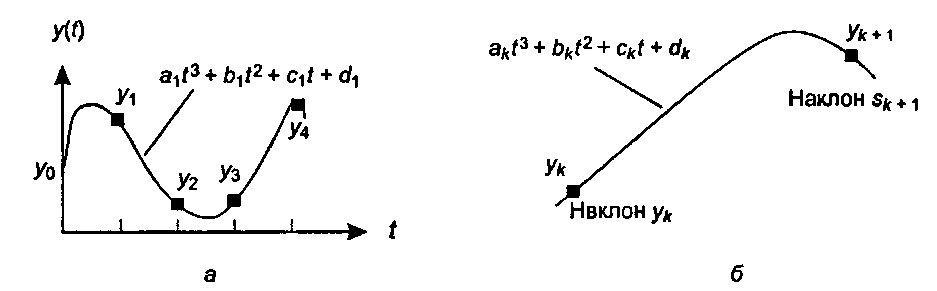
Рис. 11.40. у-компонент интерполирующей кривой

11.10. Краткое знакомство с интерполяцией Обозначим через зА значение производной этой функции в точке ук, то есть г/'4(0) - 54. Как мы увидим далее, в некоторых случаях значения «4 заданы (то есть введены пользователем), а иногда вычисляются, исходя из других требуемых свойств кривой. И снова мы спрашиваем"opengl1_808.html">⇐ Предыдущая| |Следующая ⇒