Пример 11.9.3. Исследование влияния весовых множителей На рис. 11.38, а приведена кубическая B-сплайн кривая на базе шести контрольных точек (с равноотстоящими узлами). Эта кривая является обычным нерациональным B-сплайном (или, что то же самое, NURB с одинаковыми весами w.). На рис. 11.38, б показано, что получится, если веса сделать неодинаковыми: кривая в большей степени притягивается к точкам с большим значением веса. (Что будет, если вес какой-нибудь точки обратится в нуль?)
NURBS приобрели популярность среди дизайнеров кривых из-за их универсальности и гибкости. Поскольку они включают в себя как частный случай B-сплайны, с помощью одного алгоритма генерирования кривых можно создавать обширное семейство разнообразных форм, в том числе конические сечения. Таким образом, дизайнеру не требуется инструментарий из многих алгоритмов для создания кривых, а достаточно лишь одного метода.
Существует целый ряд других технологий построения кривых, причем некоторые из них предоставляют пользователю даже больший контроль над формой кривой. Например, можно варьировать рае-стояния между узлами в узловом векторе (здесь они приняты одинаковыми) или добавлять к имШи щимся данным дополнительные «ложные» («ghost») точки с целью управлять поведением кривой в концевых точках. Читателю, интересующемуся различными обобщениями, следует обратиться к одному из многочисленных источников по B-сплайнам, таким как [Härtels, 126, Farin, 60].
11.10. Краткое знакомство с интерполяцией
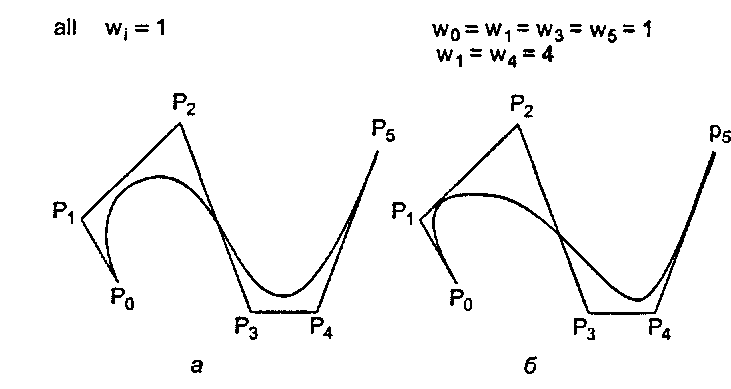
Рис. 11.38. Влияние неодинаковых весов на NURBS-кривую: а) w, = 1; б) w0 = w, = w3 = w5 = 1, w, = w4 = 4
Практическое упражнение
11.9.4. Действительно ли это окружность?
Покажите, что NURBS-кривая, описанная в примере 11.9.2, действительно является окружностью. Для этого найдите выражения для полиномов базисных функций в каждом межузловом интервале, вычислите значение выражения ^(r) + y2(t) и покажите, что оно равно единице для всех t.
11.10. Краткое знакомство с интерполяцией Иногда дизайнеру нужно, чтобы кривая, получающаяся в результате работы алгоритма, проходила через все контрольные точки. Такая кривая может показаться более естественной, чем кривая, полученная при использовании алгоритма, который только «притягивает» ее к контрольным точкам. Однако мы еще увидим, что если принудить кривую проходить через набор точек, то это может привести к кривым с недопустимо малым локальным контролем или к нежелательным дополнительным «извивам» между контрольными точками. Несмотря на такие ограничения, мы все же хотим обеспечить дизайнера инструментальными средствами для тех случаев, когда интерполяция является предпочтительной.
