11.9.3. Формирование NURBS-кривых в однородных координатах

Рассмотрим формирование В-сплайн кривой на базе контрольных точек Рк, взвешенных с помощью определенного набора весов {wk}. Такая В-сплайн кривая формируется в однородных координатах в следующем виде:

* = о где символом Рк обозначена контрольная точка Рк в однородных координатах (то есть для ЗБ-точки О Напишите выражения для отдельных KOMnoHeHTOBx(t),y(t),z(t),w(t) для R(t) = [x(t),y(t),z(t),w[t)) , уделяя особое внимание выражению для w(t).

О Преобразуйте равенство (11.72) в обычные координаты, разделив его на w(t). Покажите, что в результате получается равенство:

P(t) = -L-. (11.73)
* = 0

О Покажите, что уравнение (11.73) имеет ту же форму, что уравнения (11.68) и (11.69). Пример 11.9.1. Получение конических сечений Для рассмотрения частного случая уравнения (11.14) положим т - 3 (квадратичные В-сплайны) и выберем узловой вектор так, чтобы получились полиномы Бернштейна (Как именно?) Теперь, полагая и0 = г»! = 1ии1 = »; получим уравнение (11.14).

Пример 11.9.2. Построение правильной окружности Существует несколько способов построения правильной окружности с помощью NURBS-кривой [Piegl, 167]. Рассмотрим основной метод, в котором применяются В-сплайны на базе семи контрольных

точек. На рис. 11.37, а показаны контрольные точки Р0.....Р6, лежащие на квадрате, а также генерируемая полная окружность. Указаны также нужные значения весов; заметим, что они равны 1 или 1/2. Узловой вектор имеет следующий вид:

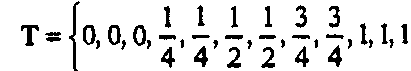
Создание кривых и поверхностей

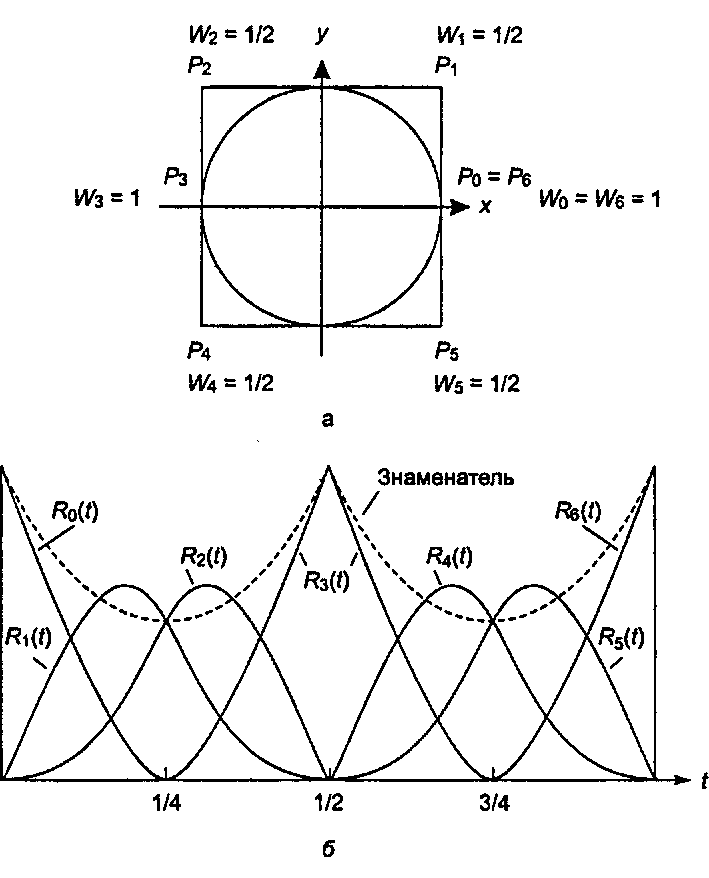
Рис. 11.37. Построение правильной окружности: а) квадрат из семи взвешенных контрольных точек; б) семь базовых функций Обратите внимание на узлы двойной кратности. На рис. 11.37, б приведены семь базисных функций, которыми взвешиваются контрольные точки. Форма кривой общего знаменателя для каждой функции Rk(t) показана на рисунке пунктиром. В упражнении 11.9.4 в конце раздела показан процесс получения формул для каждой базисной функции на каждом межузловом интервале; вы сможете убедиться, что для всех г выполняется равенство д^(г) + y2(t) - 1.

⇐ Предыдущая| |Следующая ⇒