для каждого £е[г0, гя + Как мы уже видели для случаев низких порядков, это утверждение может быть доказано методом индукции, исходя из уравнения (11.58).

6. Кривые на базе В-сплайнов аффинно инвариантны. Для преобразования В-сплайн кривой мы просто преобразуем каждую контрольную точку и генерируем новую кривую на базе преобразованных контрольных точек. Чтобы доказать это, просто заметим, что В-сплайн кривая является аффинной суммой точек и что при аффинных преобразованиях аффинные комбинации сохраняются.

7. В соответствии со свойством 5, В-сплайн кривая является выпуклой комбинацией своих контрольных точек и поэтому лежит внутри их выпуклой оболочки. Возможно более сильное утверждение: при любом значении г только т В-сплайн функций «активны» (то есть отличны от нуля). Таким образом, для любого г кривая должна лежать внутри выпуклой оболочки не более т последовательных активных контрольных точек. На рис. 11.35 показана квадратичная В-сплайн кривая на базе стандартного узлового вектора. При каждом значении с активны не более трех контрольных точек, поэтому соответствующие выпуклые оболочки являются треугольниками. При возрастании £ функция Р(г) постепенно переходит из одной выпуклой оболочки в следующую по мере того, как становится активной очередная стыковочная функция. При каких значениях £ кривая входит в закрашенную выпуклую оболочку и выходит из нее (см. рисунок)?

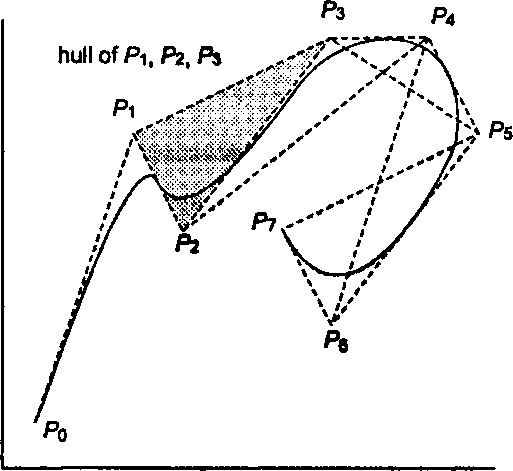
Рис. 11.35. Выпуклые оболочки для квадратичной В-сплайн кривой Выпуклые оболочки т контрольных точек обычно занимают области меньшего размера, чем оболочка всех контрольных точек. Поэтому данная кривая «захватывается» в меньшую область, Глава И. Создание кривых и поверхностей чем кривая Безье. Узкий диапазон поддержки В-сплайнов не только предоставляет дизайнеру1 локальный контроль, но также позволяет глубже осмыслить природу кривой.

8. В-сплайн кривые обеспечивают линейную точность"opengl1_800.html">⇐ Предыдущая| |Следующая ⇒