11.7.2. Поддержка В-сплайна Покажите, что функция га(с) всегда равна нулю вне интервала [tk, tk + J, так что поддержка Я-сплайна т-то порядка равна тп диапазонов узлового вектора. Покажите также, что функция m(t) неотрицательна для всех значений t.
11.7.3. Квадратичные В-сплайн функции в сумме всегда равны единице Мы уже показали, что линейные В-сплайн функции в сумме равны единице. Покажите, что это также верно для квадратичных В-сплайнов.
Подсказка. При решении вам может помочь такая последовательность шагов: вы хотите показать, что
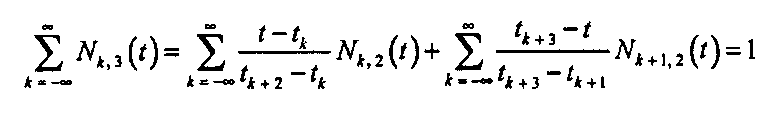
для всех значений г. (обратите внимание, что суммирование идет от -«» до °°); в этом выражении непосредственно применено уравнение (11.58). Сделайте замену переменных во второй сумме (&-> к - 1),
Создание кривых и поверхностей
затем сгруппируйте суммы в одну, учитывая, что коэффициент при 2(г) всегда равен единице. Поскольку к B-сплайнам второго порядка всюду прибавляется единица, то на этом доказательство закончится.
11.7.4. Вычисление кубического В-сплайна Проверьте формулы уравнения (11.64) для кубического B-сплайна на базе равноотстоящих узлов. Кроме того, вычислите первую и вторую производные кубического B-сплайна и покажите, что они непрерывны всюду.
11.7.5. Ручной прогон Прогоните вручную алгоритм вычисления значения функции ЛГ3 2(2.6), приведенный в листинге 11.1, для случая равноотстоящих узлов, где tt = i.
11.7.6. Периодические B-сплайн кривые Покажите, что кривая н<)=£^o.,„((<-*)mod(i+i)) (H.66)
* = 0на базе (1+1) контрольной точки и B-сплайнов т-го порядка является замкнутой и, следовательно, периодической по г.
11.7.2. Использование кратных узлов в узловом векторе До сих пор мы использовали только B-сплайны на базе равноотстоящих узлов. Изменяя расстояние между узлами, дизайнер получает значительно больший контроль над формой результирующей кривой. Главный вопрос состоит в следующем: что произойдет с формами стыковочных функций, если два узла окажутся очень близко друг к другу? Рисунок 11.31 показывает ситуацию, в которой узловой вектор равен Т = (0,1,2,3,3 + е, 4 + е,…), где е - малое положительное число. Тогда «кусок» каждого кусочного полинома, лежащего в интервале [3,3 + е], «вжимается» в очень узкий диапазон. Очевидно, что стыковочные функции при этом больше не будут собственными смещенными версиями. Если положить е равным нулю, то этот диапазон полностью исчезнет, и при г - 3 будет иметь место кратный узел (multiple knot). Рассматриваемый узел будет иметь кратность 2. На рис. 11.32 показаны результирующие стыковочные функции. Теперь две линейные формы B-сплайнов при t = 3 имеют разрыв (рис. 11.32, б), а квадратичные формы - разрывную производную (рис. 11.32, в). В общем случае в кратном узле i-гладкая кривая превращается в (i - 1)-гладкую кривую. Кубические B-сплайн кривые (рис. 11.32, г) являются повсюду 1-гладкими, однако не 2-гладкими при г = 3. Заметим, однако, что если (см. рис. 11.32, в) использовать квадратичные B-сплайны, то кривая будет интерполировать контрольную точку Р2, поскольку стыковочная функция N2 3(г) при г = 3 равна единице, а все остальные стыковочные функции в этой точке равны нулю. Вообще говоря, когда t приближается к узлу, имеющему кратность больше единицы, возникает сильное притяжение к управляющей (governing) контрольной точке. (К какой именно?)
