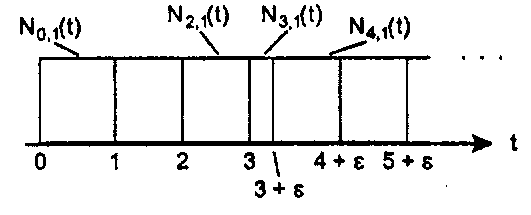
Рис 11.31. Сближение узлов Далее, квадратичные сплайны становятся разрывными вблизи узла кратности 3. Кубические сплайны имеют разрывную производную вблизи узла кратности 3, причем они также интерполируют одну из контрольных точек. Назначая кратность каждого узла, дизайнер может таким способом изменять форму кривой. Как уравнение (11.58), так и фрагмент кода из листинга 11.1 без каких-либо изменений могут работать с узловыми векторами, содержащими кратные узлы. Как уже упоминалось, некоторые

11,7. Базисные функции В-сплайнов знаменатели в этом уравнении могут обращаться в нуль, однако в программе такая ситуация учитывается автоматически, поэтому никаких корректировок кода делать не нужно.

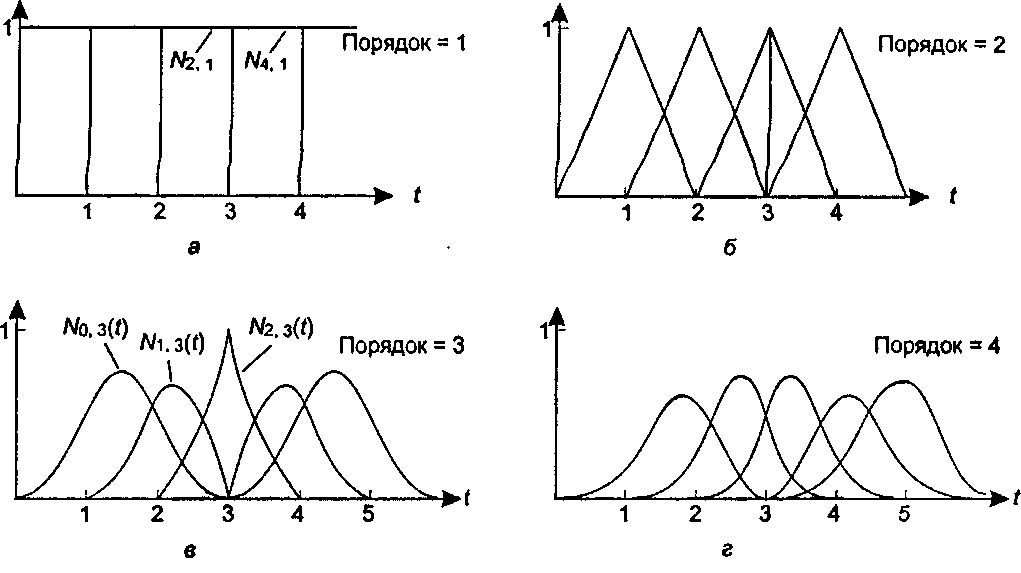
Рис. 11.32. Формы В-сплайнов вблизи узла кратности 2

11.7.3. Незамкнутые В-сплайн кривые"opengl1_795.html">⇐ Предыдущая| |Следующая ⇒