11.6. Нахождение лучших стыковочных функций

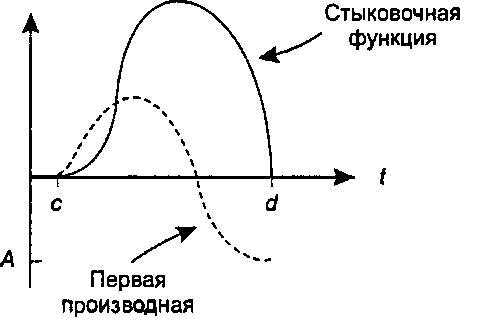
(при г - а1), ее производная имеет разрыв, совершая резкий скачок от А до нуля. Такая функция является 1-гладкой всюду, кроме точки с - й. Тогда и кривая, использующая эту стыковочную функцию, не будет 1-гладкой при г - й. Поэтому для стыковочных функций желательно, чтобы они были гладкими внутри интервала, а также начинались и заканчивались с нулевым значением производной.

Рис. 11.21. Предполагаемая стыковочная функция и ее производная Некоторые из форм, изображенных на рис. 11.20, начинаются и заканчиваются там, где их производная равна нулю, а другие - нет. Те формы, которые начинаются и заканчиваются внутри интервала [0, 1], делают это с нулевой производной, поэтому кривая V(t) будет 1-гладкой внутри интервала (0, 1). Для производных допускается разрыв на концах интервала [0, 1], поскольку мы никогда не используем значения г, меньшие нуля или большие единицы.

11.6.3. Кусочно-полиномиальные кривые и сплайны

Начнем с поиска хороших кандидатов на роль стыковочных функций, например, среди полиномов низкого порядка. Существует ли, например, такой кубический полином, форма которого показана на рис. 11.22 и который удовлетворял бы всем нашим требованиям? Для изучения этого вопроса зададим функцию:

R(t) = at3 + bt2 + ct + d

и посмотрим, можно ли подобрать коэффициенты так, чтобы функция R(t) и ее первая производная обращались в нуль при с = 0 и при t - 1. Это требование накладывает на коэффициенты следующие четыре условия: Д(0)-«7-0;

R(l) = a + b + c + d = 0; Д'(0) - с = 0;

= За + 2Ь + с - 0.

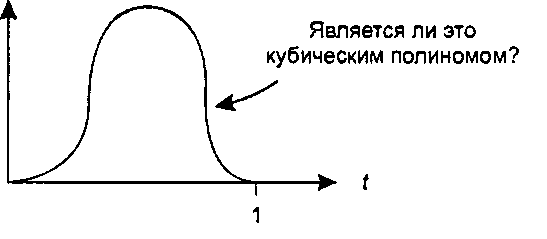
Рис. 11.22. Можно ли подыскать такой кубический полином?

К сожалению, из этих условий следует, что а = £ = с = г/=0, следовательно, подобной формы не существует. У кубической формы недостаточно гибкости, чтобы «изогнуться» так, как нам это требуется. (В упражнении 11.6.1 исследуется вопрос, подойдет ли для этой роли полином четвертого порядка.)

Создание кривых и поверхностей

С целью достижения большей гибкости попытаемся «составить» вместе несколько полиномов низкого порядка. Такие кривые определяются различными полиномами на различных интервалах изменения t и носят название кусочных полиномов (piecewise polynomials). Примерная форма g(t), приведенная на рис. 11.23, поможет нам при введении некоторой терминологии. Видно, что кривая g(t) состоит из трех полиномиальных сегментов (segments), определяемых следующими формулами"opengl1_783.html">⇐ Предыдущая| |Следующая ⇒