Пенроуз показал, что при этих ограничениях можно укладывать змеи и дротики на плоскости бесконечным числом способов, однако каждая такая мозаика должна быть непериодической. (Для этого нужно потрудиться и вырезать примерно 100 змеев и около 50 дротиков, раскрасить их, после чего можно раскладывать мозаику.) Он также доказал, что соотношение змеев и дротиков в любой бесконечной мозаике в точности равно золотому соотношению ф. Из того, что ф является иррациональным числом, следует доказательство апериодичности любой мозаики; так как в периодической мозаике соотношение должно быть рациональным.

Пенроузу и Конвею удалось разработать ряд замечательных теорем, касающихся мозаик; все они превосходно описаны у Мартина Гарднера (Martin Gardner [Gardner, 78]). Например, всякий раз, когда черная или серая кривая становится замкнутой, она должна иметь пентагональную симметрию, причем вся область внутри такой кривой должна обладать пятикратной симметрией. Более того, в большинстве мозаик все кривые являются замкнутыми: в узоре может быть не более двух незамкнутых кривых каждого цвета.

Приближение к бесконечности

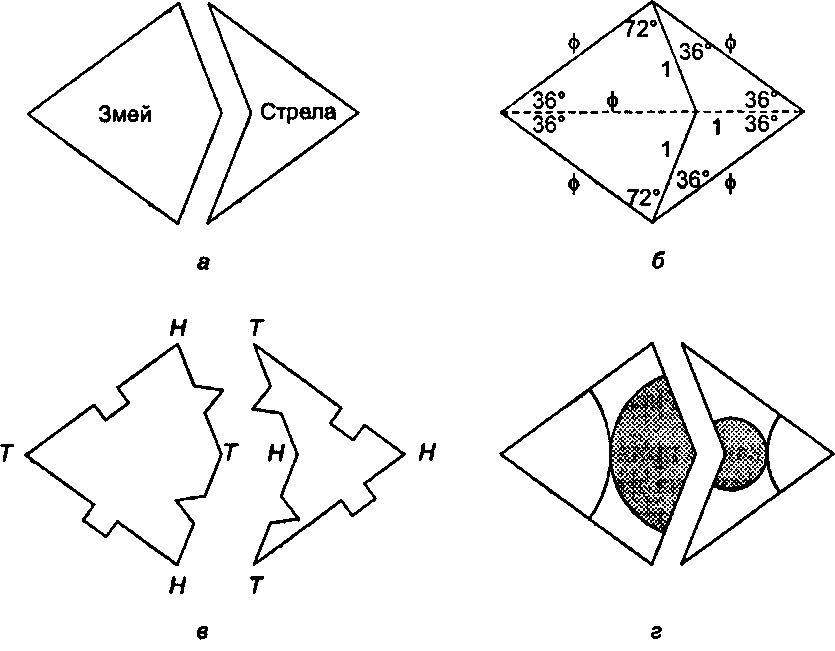
Рис. 9.56. Змей и дротик Пенроуза Разработайте алгоритм для рисования мозаик Пенроуза и выполните его. (Замечание"opengl1_667.html">⇐ Предыдущая| |Следующая ⇒