9.10.3. Из треугольников На рис. 9.57 показано, как можно превратить равнобедренный треугольник в девятиугольник («enneagon»), обладающий свойством без зазоров совмещаться со своей полуповернутой версией, образуя восьмиугольник [Gardner, 78].

О Покажите, что такой восьмиугольник всегда образует на плоскости периодическую мозаику. О Каким условиям должны удовлетворять ребра Л и В, чтобы они образовали девятиугольник? О Докажите, что существует бесконечное множество различных форм девятиугольника.

Тематическое задание 9.8. Фрактализация кривых

Уровень сложности II.

Напишите и выполните приложение, которое рисует «фрактализованные» линии. Пользователь задает ломаную линию, как обычно, с помощью мыши, после чего каждый отрезок этой ломаной рисуется в фрактализованном виде. Предоставьте пользователю возможность вводить значения различных ис9.10. Тематические задания пользуемых параметров (см. табл. 9.1). При выполнении своей программы поэкспериментируйте с различными величинами. Испытайте различные ломаные линии, представляющие собой острова, области или страны, и посмотрите, придает ли им фрактализация естественный вид.

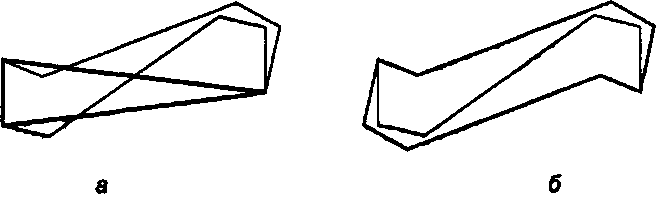
Рис. 9.57. Девятиугольник и пара фрагментов, образующих периодическую мозаику

Тематическое задание 9.9. Моделирование фрактализованных гор

Уровень сложности III.

Для создания сложнейших «фрактальных гор» можно применить процесс фрактализации, сходный с тем, который использовался при «взлохмачивании» прямой линии. На рис. 9.58 показана последовательность этого процесса. Начинаем с треугольника ABC, лежащего в плоскости ху, затем смещаем вертикально три средние точки а, Ь, с на случайные величины, формируя «штыри», поднимающиеся с пола. Теперь соединяем вершины этих штырей между собой и с исходными вершинами, чтобы образовать четыре треугольных микрограни a'b'd, а'Ь'С и т. д. Повторяем этот процесс. Тогда каждая микрогрань будет заменяться на четыре новых микрограни тем же способом"opengl1_668.html">⇐ Предыдущая| |Следующая ⇒