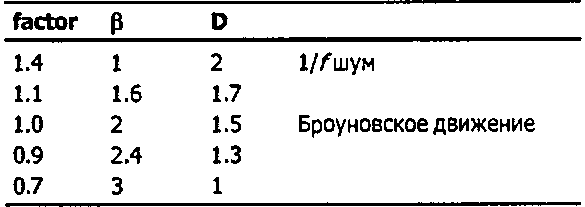
factor = 2«-&2К (9.24)
Таким образом, с ростом Р масштабный множитель уменьшается. Некоторые его характерные значения приведены в табл. 9.1.
Таблица 9.1. Зависимость множителя и D от (3
' В некоторых работах 1 //шумом называют все семейство «шумов» со спектральной плотностью 1 /Р для всех Р в пределах от 0,5 до 1,5 [Peitgen, 158].
9,8. Случайные фракталы
Отметим, что factor = 1 при Р = 2, и в этом случае относительное среднеквадратическое отклонение не изменяется от уровня к уровню. Это соответствует модели броуновского движения. Для устойчивых кривых, для которых Р > 2, factor < 1, поэтому среднеквадратическое отклонение убывает от уровня к уровню: смещения колен становятся все менее и менее статистически выраженными. С другой стороны, когда Р < 2, образуются неустойчивые кривые: для них factor больше 1, вследствие чего среднеквадратическое отклонение возрастает от уровня к уровню, так что колена становятся все более и более отчетливыми.
Листинг 9.10. Рисование фрактальной кривой (псевдокод)
double MinLenSq. factor:
// global variables// глобальные переменные
void drawFractal(Point2 A, Point2 B)
{
double beta. StdDev;user inputs beta. MinLenSq. and the initial StdDev II пользователь вводит beta. MinLenSq и начальное StdDev factor = pow(2.0.(1.0 - beta)/2.0): cvs.moveTo(A): fract(A. B. StdDev);
}Фрактал может быть нарисован методом, приведенным в листинге 9.10. В этой подпрограмме factor вычисляется с помощью функции pow(…) из библиотеки С++.
На рис. 9.49 показаны примеры фрактальных кривых, построенных на базе отрезка единичной длины при различных значениях показателя степени р. (Для этих рисунков задано minLenSq = 0,05 и StdDev = 0,1.) Для каждого значения Р было сгенерировано по пять фрактальных кривых с целью показать возможные вариации. Следует отметить четко выраженную зависимость вида фракталов от значения р.
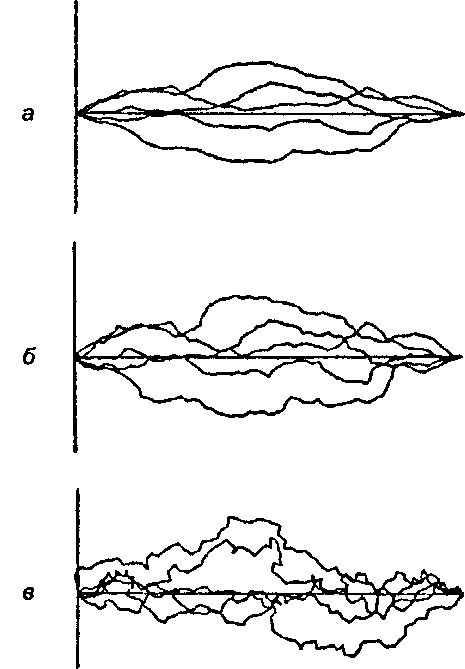
Рис. 9.49. Пример фрактальных кривых: а) р = 2,4; б) р = 2; в) р = 1,6
Приближение к бесконечности
На рис. 9.50 показано, как можно фрактализовать произвольные ломаные линии. Предлагается простое средство «разлохмачивания» формы, чтобы ее извивы выглядели естественно. На этом рисунке была произведена грубая оцифровка береговой линии штата Флорида, так что этот штат аппроксимирован всего 20 точками (см. рис. 9.50, а). Затем каждый из отрезков береговой линии Флориды был подвергнут фрактализации, а внутренние границы штатов, которые должны быть прямыми линиями, были оставлены без изменения. Чрезвычайно интересно фрактализовать полигоны, представляющие известные географические объекты: острова, страны, континенты, и увидеть, насколько естественно могут выглядеть их границы. Можно фрактализовать и другие формы, например животных или макушку человеческой головы, - с целью придания им естественного вида.
