Мотив k-й кратности (k-rep tile) - это произвольный полигон Р, который можно разбить на k конгруэнтных частей, каждая из которых подобна Р [McGregor, 138]. (Будем говорить также, что такой полигон обладает «£-й кратностью».) На рис. 9.23 показано пять простых примеров. Тримино (triomino) является полимино 4-й кратности, а сфинкс (sphinx) - полиамондом. Сфинкс - это единственный известный Пентагон 4-й кратности.
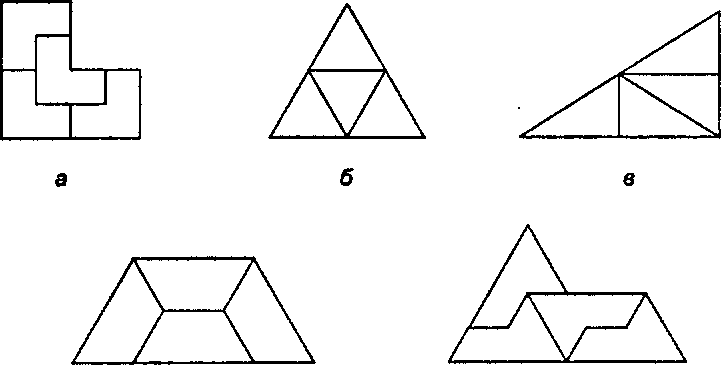
г а Рис. 9.23. Примеры рептилий: а) тримино; б) равносторонний треугольник; в) треугольник 30-60-90; г) трапеция; д) сфинкс
«Самовоспроизведение» рептилий возможно в двух противоположных направлениях: в сторону бесконечно большого и в сторону бесконечно малого. Можно составить вместе четыре сфинкса, чтобы получить сфинкса большего размера. Этот процесс можно повторять бесконечно и получить сколь угодно большого сфинкса. Подобным же образом можно нарисовать внутри каждого сфинкса маленьких сфинксов и повторять эту регрессию бесконечно для получения сколь угодно малых сфинксов. (Проверьте эти утверждения для каждого из пяти приведенных примеров.)
Приближение к бесконечности
Отметим, что любой треугольник является рептилией 4-й кратности: нужно просто соединить середины трех его сторон. Это показывает, что любой и-угольник также является рептилией, поскольку его всегда можно разбить на п треугольников. Кроме того, для любого заданного k существует рептилия k-й кратности: это параллелограмм с соотношением сторон liyfk. (Как выглядит этот параллелограмм?) Оказывается, единственная известная рептилия 7-й кратности - это такой параллелограмм.
Рисование рептилий Представляется удобным рассуждать о рептилиях в терминах «поколений»: мотив k-й кратности можно рассматривать как «родителя» k «потомков»; в таком случае у каждой рептилии имеется один родитель. Для того чтобы нарисовать рептилию, мы просто рисуем ее потомков, в силу чего данный процесс естественным образом является рекурсивным. Эту рекурсию можно остановить или по достижении заданной глубины (числа произведенных поколений), или когда размер потомков станет «достаточно малым».
