В = Щ (9.1)
log -Чему же равна дробная размерность кривой Коха? При переходе от одного поколения к следующему из каждого предыдущего отрезка создается N = 4 отрезка, а их длины получаются из длин отрезков предыдущего поколения при умножении их на множитель г = 1/3, поэтому
£» = log(4)/log(3) = l,26.Размерность кривой Коха действительно находится между 1 и 2. Если кривая А обладает большей размерностью D, чем кривая В, то кривая А обязательно будет более «извилистой», чем кривая В; это означает, что она меньше похожа на линию и ей присуща большая «заполняемость плоскости». Фрактальная кривая и в самом деле может «заполнить плоскость» и в силу этого приобрести размерность два, как мы увидим позднее. Такие кривые называются кривыми Пеано1.
Усложнение каждого очередного поколения кривой для создания следующего может осуществляться и многими другими способами. На рис. 9.4 приведено три примера: квадратная кривая Коха, так называемый «дракон» («dragon») и кривая Госпера, названная по имени Дэвида Госпера (David Gosper),
1 Названы в честь Джузеппе Пеано (Giuseppe Реапо, 1858-1932), итальянского логика и математика.
9.3. Создание строк и кривые Пеано американского математика, родившегося в 1943 году. В квадратной кривой Коха отрезки в каждом поколении дробятся на восемь отрезков с длиной, равной одной четверти исходного отрезка, следовательно, ее размерность Э = log(8)/log(4) = 1,5. (Пунктирными линиями показано предыдущее поколение с наложенным на него новым поколением.) Что касается кривой дракона, то у нее каждая прямая замещается двумя прямыми длиной 1/^2 , тогда £) = 1о§(2)у/1о§(72) = 2. У кривой Госпера каждый отрезок прямой АВ замещается семью отрезками длиной \/77 , поэтому снова размерность Э = 2. Ниже рассматриваются специальные приемы рисования таких кривых.
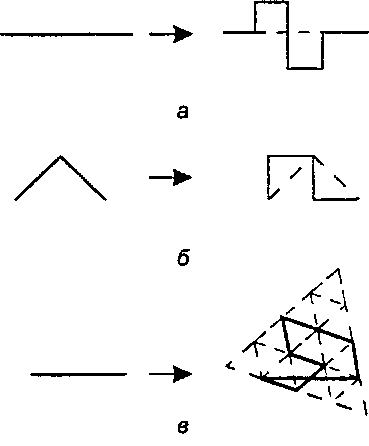
Рис. 9.4. Другие приемы усложнения прямых: а) квадратная кривая Коха; б) дракон (dragon); в) кривая Госпера
9.3. Создание строк и кривые Пеано
