аналогично может быть получено выражение для £|еЛ. Отметим, что х|сЛ и £1еГ[ имеют один и тот же знаменатель: линейная интерполяция между значениями 1/я4 и 1/&4. Числители являются линейными интерполяциями текстурных координат, деленных на а4 и 64. Эту технику иногда называют «линейной рациональной» визуализацией [НескЬегг,, 105] или «гиперболической интерполяцией» [ВПпп, 24]. Для эффективного вычисления координат (х, 0 по мере роста/необходимо сохранять значения $л/я4,5й/&4> гд/а4, Ьд/Ь^, 1/а4, 1/64, так как они остаются постоянными от пиксела к пикселу. Числитель и знаменатель могут быть найдены в приращениях для каждого у, в точности так, как мы это делали в закрашивании Гуро. (См. уравнение (8.14).) Однако для нахождения х|еЛ и Ьш нам все же придется выполнить явное деление каждого значения у.
(8.19)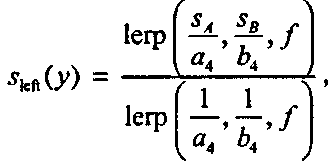
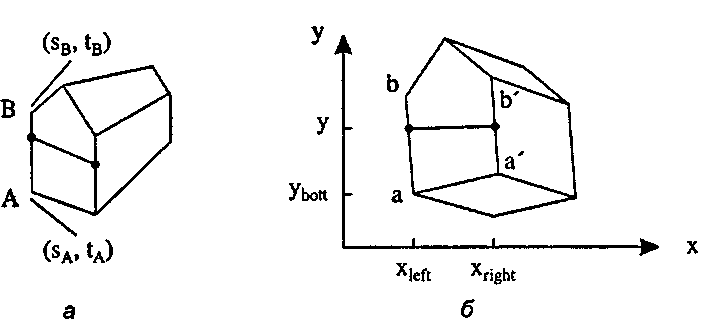
Рис. 8.45. Визуализация текстуры на грани
8.5. Добавление текстуры к граням Пара координат (sright, cright) вычисляется аналогично. Знаменатели этих двух компонентов содержат величины а4 и b'v которые получаются из проецированных точек а' и Ъ'.
После нахождения (slcft, r|eft) и (srig]it, fright) данную строку развертки можно закрашивать. Для каждого х от xMt до xrjght находятся координаты s и t - снова посредством гиперболической интерполяции. (Какое выражение имеет s в зависимости отх?)
Включение в графический конвейер
Как подключить нужное применение гиперболической интерполяции для правильной визуализации текстуры? И нужно ли при этом уточнять этап отсечения? Как мы сейчас увидим, мы должны посылать в графический конвейер дополнительную информацию и вычислять несколько иные значения, чем мы полагали до сих пор.
На рис. 8.46 приведена детализированная схема графического конвейера. На этой схеме отмечены некоторые точки и показано, какая информация содержится в каждой такой точке. Каждая вершина V связана с парой текстурных координат (s, г), а также с нормалью в этой вершине. Вершина преобразуется с помощью матрицы моделирования-вида (а соответствующая нормаль умножается на обратную транспонированную матрицу), в результате чего получаются вершина А - (Л,, А2, А3) и нормаль п' в координатах глаза. Эта нормаль используется в вычислениях закрашивания, в результате чего получается цвет с = (cr, cg, сь). К вершине А по-прежнему привязаны текстурные координаты (sA, tA) (совпадающие с координатами (s, t)). После этого вершина А подвергается перспективному преобразованию, в результате чего получается а - (а,, а2, а3, а4). Текстурные координаты и цвет с не изменяются.
