Факт: если матрица М является аффинной, то равные шаги по прямой аЪ соответствуют равным шагам по прямой АВ.

Если же матрица М представляет собой перспективное преобразование из координат глаза в координаты отсечения, то четвертые компоненты а4 и 6, уже не равны единице. Такая матрица Мрассматривалась в главе 7; ее основная форма, заданная равенством (7.10), имеет вид:

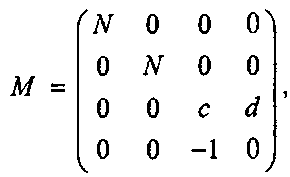
где cud- константы, отвечающие за правильную псевдоглубину. Чему же равно выражение М(А, 1)г для этой матрицы? Оно равно а = (NAV NA2, сА3 + d, -vl3), и главное состоит в том, что о, - -Ау Это и есть координата точки вдоль оси z в координатах камеры, иначе говоря, глубина этой точки по отношению к глазу.

Таким образом, относительные размеры о, и й4 лежат в основе перспективного укорачивания отрезка прямой: они несут информацию о глубинах точек А к В вдоль нормали к плоскости просмотра камеры. Если точки А и В имеют одинаковую глубину (то есть лежат в плоскости, параллельной плоскости просмотра камеры), то искажение перспективы вдоль этого отрезка отсутствует и части g и /действительно совпадают. На рис. 8.44 показано в разрезе, как лучи от глаза, проходящие через равноотстоящие точки (с равными приращениями по /) на плоскости просмотра, попадают в уже неравноотстоящие точки на исходной трехмерной грани. На рисунке показан случай, когда точка А ближе точки В, откуда следует, что о, < &4, поэтому приращения по g возрастают по мере обхода грани от А к В.

Визуализация граней для усиления реалистичности

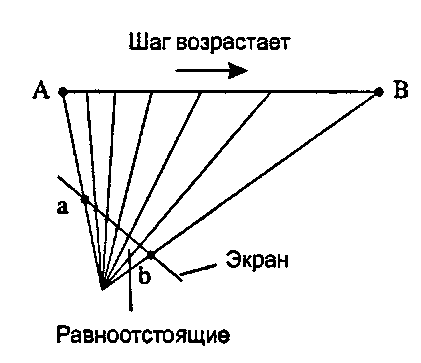
Рис 8.44. Значения а4 и Ь4 зависят от глубин точек Инкрементная визуализация изображений Соединим теперь все вышеизложенное вместе и найдем соответствующие текстурные координаты (х, £) в каждой точке визуализируемой грани. На рис. 8.45 показана грань сарая. Концевые точки левого ребра спроецированной грани равны а и Ь. Данная грань простирается от хш до хг. ^ вдоль строки развертки у. Нам нужно найти соответствующие текстурные координаты (5|еЛ, г|еЛ) и (^8к, для привязывания их соответственно к точкам от хкк до хг.щЫ, которые мы затем сможем интерполировать вдоль строки развертки. Рассмотрим нахождение $М1(у) - значения $|еЛ вдоль строки развертки у. Мы знаем, что текстурная координата $Л привязана к точке а, а $в привязана к точке Ь, поскольку эти величины передаются через графический конвейер вместе с вершинами А и В. Если строка развертки у является частью / расстояния между у^ и ущ, так что/=(у- УЫ^)/(УЩ - т0 из равенства (8.18) следует, что соответствующая текстурная координата равна"opengl1_566.html">⇐ Предыдущая| |Следующая ⇒