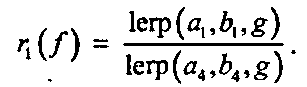
(8.15)Но поскольку по определению г(/) - 1егр(я, Ь,/), у нас имеется и другое выражение для первого компонента:
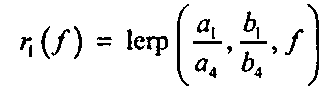
(8.1«)Аналогично могут быть получены выражения для г,(/) и г3(/). (Чему они равны?) Приравниваем эти две формулы для г,(/) и после алгебраических преобразований получаем нужное соотношение между величинами /и &
(8.17)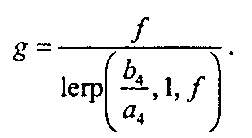
Следовательно, точка /?(#) отображается в точку г(/), однако g и / не являются одними и теми же долями. Доля g совпадает с/при/=0ипри/=1, однако рост g с ростом / определяется знаменателем, зависящим от отношения Ь4/а4. Если же а4 и Ь4 равны между собой, то g совпадает с /. (Проверьте это.) На рис. 8.43 показана зависимость £ от/ для различных значений Ь4/а4.
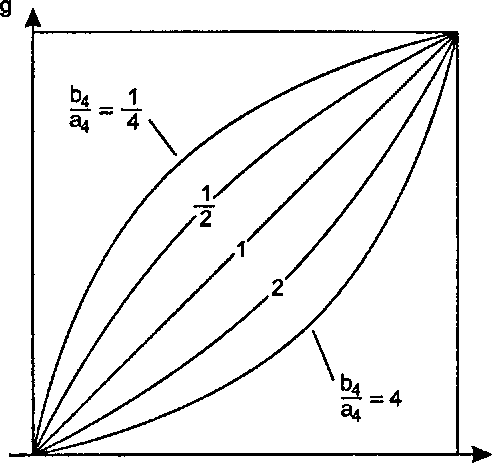
Рис. 8.43. Зависимость д от f
8.5. Добавление текстуры к граням Теперь мы можем сделать заключительный шаг и показать, где расположена точка і?^), отображаемая в точку г(/) на трехмерной грани"images/tmp8E4A-568.png">
(8.18)Аналогичные результаты получаются для компонентов /?2 и Я3 (у них тот же самый знаменатель, что у 7?,). Это и есть искомый результат; он говорит о том, какая трехмерная точка Я2, Я3) соответствует (в координатах глаза) заданной точке, лежащей на части /пути между заданными точками а и Ь в экранных координатах. Таким образом, любая величина (например, текстура), «привязанная» к вершинам трехмерной грани и изменяющаяся линейно между этими вершинами, будет вести себя таким же образом.
Имеются два интересных случая преобразования с матрицей М: О Преобразование является аффинным. О Преобразование является перспективным преобразованием. Рассмотрим каждый из этих случаев поочередно.
Когда данное преобразование является аффинным, компоненты я4 и 6, равны единице (почему?), следовательно, вышеприведенные формулы сразу упрощаются. Теперь части / и g становятся идентичными, а Я, превращается в 1егр(Л,, 5,,/). Итог такому развитию событий подводит приведенный ниже факт.
