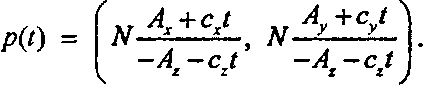
(7.5)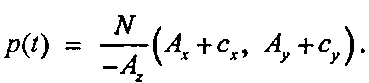
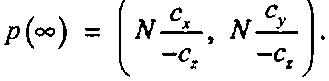
(7.6)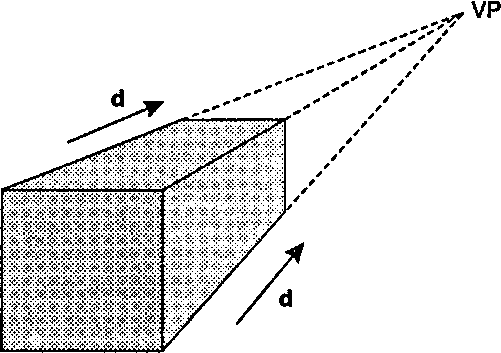
Рис. 7.18. Точка схода параллельных прямых
Трехмерный просмотр
Рисунок. 7.18 делает последнее утверждение более наглядным - на примере куба. Некоторые ребра куба параллельны"images/tmp8E4A-476.png" alt="Геометрическая интерпретация точки схода">
Рис. 7.19. Геометрическая интерпретация точки схода На рис. 7.19 предлагается геометрическая интерпретация точки схода. При взгляде сверху вниз на плоскость хг в системе координат камеры мы видим различные точки прямой АВ. Точка А проецируется в А', В - в В' и т. д. Очень удаленные точки этой прямой проецируются в УР, как показано на рисунке. Сама точка УР расположена так, что прямая, проведенная от глаза и проходящая через нее, параллельна прямой АВ. (Почему?)
Прямые, проходящие за глазом Мы уже видели, что попытка спроецировать точку, располагающуюся в плоскости глаза (в координатах глаза г = 0) приводит к тому, что знаменатель обращается в нуль, что несомненно приведет к неприятностям, если мы попытаемся спроецировать эту точку. Рассмотрим теперь проекцию отрезка прямой, одна концевая точка которого располагается перед глазом, а вторая - за ним.
Рисунок 7.20 вновь показывает вид на камеру сверху. Точка А находится впереди глаза и проецируется в А' без всяких проблем. С другой стороны, точка В располагается позади глаза и проецируется в точку В', и кажется, что она находится не на той стороне плоскости просмотра! Рассмотрим точку С, которая движется от Л к В, и нарисуем, как будет перемещаться ее проекция. По мере того как точка С движется назад к плоскости глаза, ее проекция скользит все дальше и дальше вправо по плоскости просмотра. Когда точка С достигает плоскости просмотра, ее проекция резко уходит в бесконечность, и по мере перемещения точки С позади глаза, ее проекция вновь появляется издалека в левой части плоскости просмотра. Можно сказать, что проекция «обернулась вокруг бесконечности» и вернулась с противоположного направления [ВНпп, 26]. Если бы мы попытались нарисовать такую прямую, то это вызва-
