Вид № 2. Здесь камера была перемещена так, что eye - (0,5, 0, 2), однако векторы и и п те же, что и в виде № 1. Рисунок 7.15, б показывает соответствующую проекцию.
Вид № 3. В этом случае используется камера с eye - (2, 5, 2) и look = (0, 0, 0). Результат приведен на рис. 7.17. Для наглядности на рисунке показаны мировые оси. Данная проекция показывает сарай с информативной точки зрения. В каркасной модели нелегко различить, где какие грани.
Трехмерный просмотр
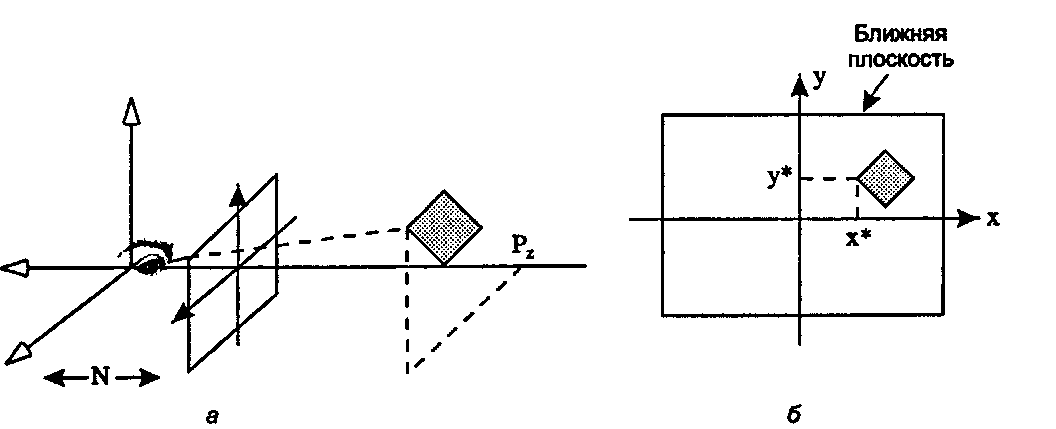
Рис. 7.16. Проекции сарая для видов № 1 и № 2
Рис. 7.17. Третий вид сарая Практические упражнения
7.4.1. Рисование куба в перспективе Нарисуйте (от руки) перспективную проекцию куба С (выровненного по осям, с центром в начале координат, с длиной сторон, равной 2) для случая, когда глаз находится в точке Е = 5 на оси г. Повторите ту же задачу для случая, когда куб С сдвинут так, что его центр находится в точке (1,1,1).
7.4.2. Где луч пересекает плоскость просмотра? (Не пропустите это упражнение)
Мы хотим вывести формулу (7.4) путем нахождения точки, в которой луч, соединяющий начало координат с точкой Р, пересекает ближнюю плоскость.
О Покажите, что если данный луч в момент времени і = О находится в начале координат, а в момент времени ґ - 1 - в точке Р, то его параметрическое представление имеет вид г(ґ) = Рі.
О Покажите, что данный луч «соударяется» с ближней плоскостью при і - Ы/(-Рг). О Покажите, что «точка соударения» (х*, у*) = (Му(-Рг), ЫРу/(-Рг)).
7.4.2. Перспективная проекция прямой линии Теперь займемся некоторыми интересными свойствами перспективных проекций, которые мы увидим при изучении проекций прямых линий.
1. Прямые линии, параллельные в трехмерном пространстве, проецируются в прямые линии, однако они не обязательно остаются параллельными. Если они не остаются параллельными, то они пересекаются в некоторой «точке схода».
7.4. Перспективные проекции трехмерных объектов
2. Прямые, проходящие за «глазом» камеры, вызывают катастрофическое «прохождение через бесконечность». (Такие прямые должны быть отсечены.)
