5. Прямые линии проецируются в прямые линии. На рис. 7.14 приводится простейшее доказательство. Рассмотрим в трехмерном пространстве прямую, проходящую через точки А и В. Точка А проецируется в А', а В - в В'. Однако проецируются ли точки между А и В в точки прямой между А' и &? Ответ будет положительным: просто рассмотрим плоскость, проходящую через точки А, В и начало координат. Поскольку любые две плоскости пересекаются по прямой линии, данная плоскость пересекает ближнюю плоскость также по прямой. Таким образом, отрезок прямой АВ проецируется в отрезок прямой А'В'.

Пример 7.4.2. Три проекции сарая Требуется весьма развитое пространственное воображение для того, чтобы представить себе, как различные камеры видят даже простой объект. В данном примере мы исследуем, как ребра сарая, определение которого давалось в главе 6 и теперь повторено на рис. 7.15, проецируются на три различные камеры. Сарай имеет 10 вершин, 15 ребер и 7 граней.

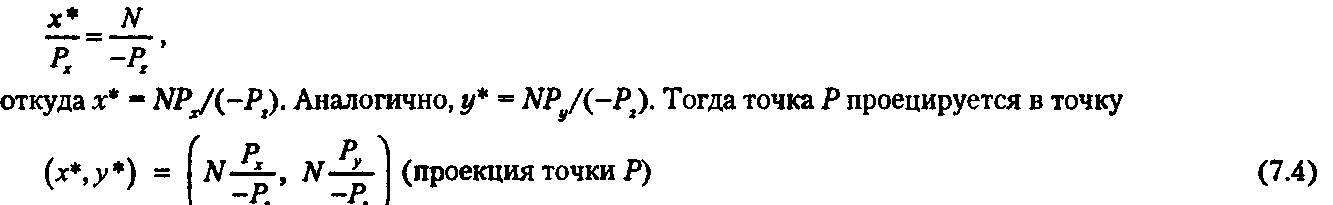
7.4. Перспективные проекции трехмерных объектов

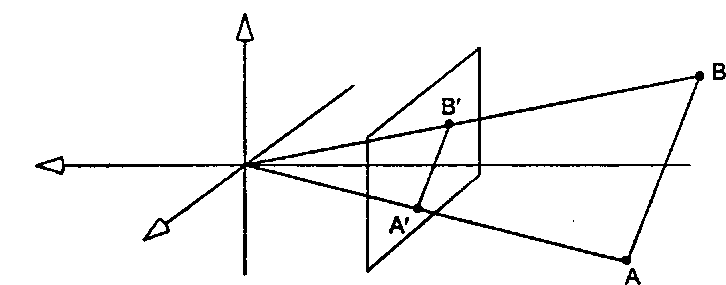
Рис. 7.14. Доказательство того, что прямая линия проецируется в прямую линию

Вид № 1. Вначале установим «глаз» камеры eye = (0,0, 2) и заставим ее смотреть вдоль отрицательной оси 2, причем и - (1,0,0), а п = (-1,0,0). Ближнюю плоскость установим на единичном расстоянии от глаза. (В этом случае ближняя плоскость совпадет с ближней гранью сарая.) В координатах камеры все точки передней стенки сарая будут иметь Рг - -1, а все точки задней стенки сарая - Рг = -2. Тогда, согласно формуле (7.4), произвольная точка (Рх, Р, Рг) на ближней стенке будет проецироваться в

F - (Рх, Ру) (проекция точки ближней стенки), а любая точка на задней стенке будет проецироваться в Р' - (PJ2, Ру/2) (проекция точки задней стенки).

Укорачивающий множитель (foreshortening factor) для точек задней стенки равен 2.

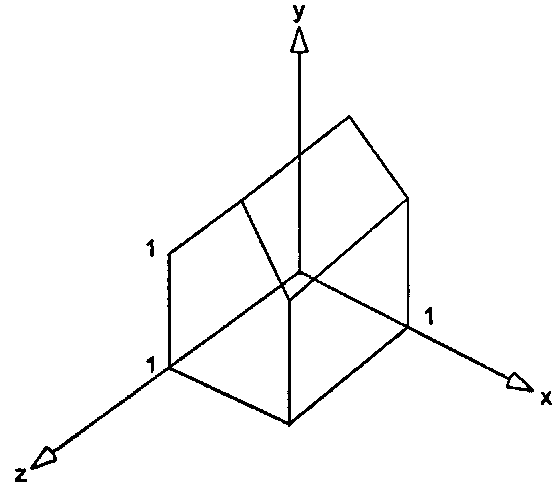
Рис. 7.15. Снова базовый сарай На рис. 7.16, а показана проекция сарая для этого вида. Отметим, что ребра задней стенки проецируются в половину их истинной длины, а также что реально параллельные друг другу в пространстве ребра сарая не обязаны быть параллельными в проекции. (В дальнейшем мы увидим, что если параллельные ребра параллельны плоскости просмотра, то они и проецируются параллельными, а параллельные ребра, не параллельные плоскости просмотра, перестают быть параллельными"opengl1_476.html">⇐ Предыдущая| |Следующая ⇒