7.4.1. Перспективная проекция точки

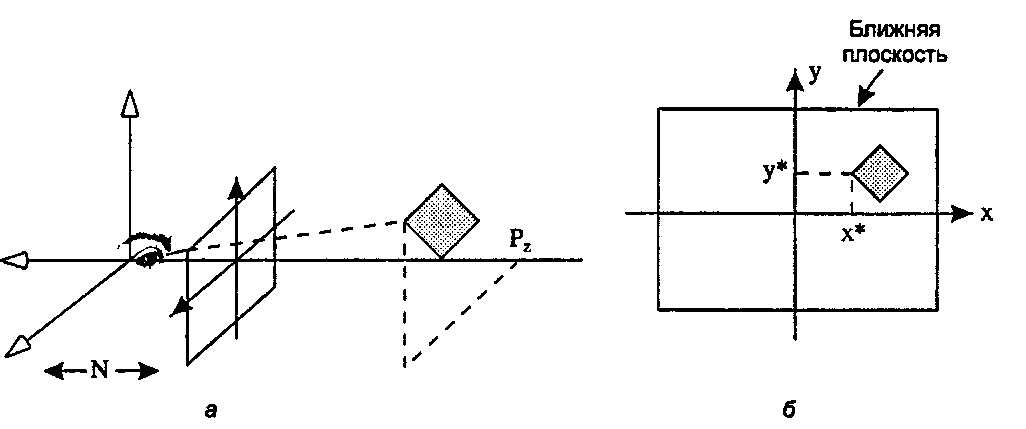
Рис. 7.13. Нахождение проекции точки Р в координатах наблюдателя

Трехмерный просмотр

Тогда первый вопрос состоит в том, чему равны1 х* и у*? Проще всего использовать подобие треугольников и убедиться в том, что х* так же относится к Рх, как расстояние ЛГк расстоянию \Рг\. Поскольку Рг отрицательно, можно утверждать, что на плоскость просмотра. Альтернативный (аналитический) метод получения этих же результатов приведен в упражнениях в конце раздела.

Пример 7.4.1

В каком месте точка Р = (1, 0,5, -1,5) располагается на плоскости просмотра камеры, ближняя плоскость которой N = 1? Решение Непосредственное применение формулы (7.4) дает (х*, у*) = (0,666,0,333).

Можно сделать некоторые предварительные замечания о том, как проецируются точки.

1. Обратим внимание на знаменатель -Р, в формуле (7.4). Его значение больше для более удаленных точек (тех, которые находятся дальше на отрицательной части оси г), что уменьшает соответствующие величины х* и у*. Это обеспечивает перспективное укорачивание (perspective foreshortening), при котором удаленные части объекта выглядят меньше, чем более близкие части.

2. Знаменатели имеют отвратительную привычку обращаться в нуль, и Pz становится равным нулю, когда точка Р располагается «в той же плоскости», что и глаз"opengl1_475.html">⇐ Предыдущая| |Следующая ⇒