Проверьте полученные файлы путем чтения каждого объекта в приложение и рисования прочитанного объекта.
Тематическое задание 6.11. Алгебраическая форма поверхностей второго порядка Уровень сложности I.
Неявные уравнения для поверхностей второго порядка можно записать в компактной и полезной матричной форме. Например, неявная форма F(x, у, z) для базовой сферы имеет вид: х2 + у2 + z2 - 1. Данное уравнение может быть записано в виде квадратичной формы (quadratic form):
6.7. Тематические задания
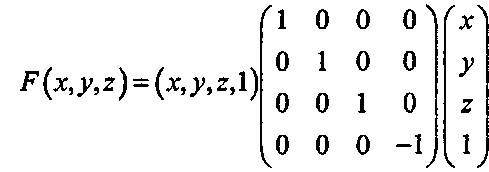
(6.51)или более компактно, с использованием однородного представления точки (х, у, г) в форме Рг= (х, у, г, 1): Р(х,у,2) = Р*К^Р, (6.52)
где /?8р11сге - матрица четыре на четыре, приведенная в равенстве (6.51). Если функция .Р равна нулю, то точка (х, у, г) находится на эллипсоиде. Неявные формы для других квадрик имеют такой же вид; различаются только матрицы /?. Например, определяющие матрицы для двуполостного гиперболоида и для эллиптического параболоида имеют следующий вид:
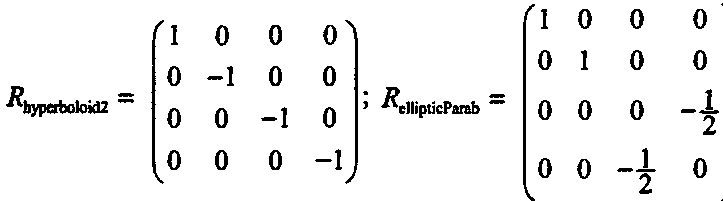
(6.53)Какой вид имеют матрицы для трех остальных форм?
Теперь вспомним из раздела «Влияние аффинного преобразования», что когда аффинное преобразование с матрицей М применяется к поверхности с неявной функцией .Р(Р), неявная функция преобразованной поверхности равна Р(М"'Р).
Покажите, что после операции преобразования квадрики ее неявная функция становится равной С(Р) = (М_1Р)ГД(М"1Р), после чего ее нетрудно преобразовать (см. приложение Б) к виду С(Р) = Р\М~*Р>.М~*)Р. Таким образом, преобразованная поверхность также является поверхностью второго порядка с другой определяющей матрицей, которая зависит как от исходного вида квадрики, так и от произведенного преобразования.
Например, для того чтобы превратить базовую сферу в эллипсоид, простирающийся по х от -а до а, по у от -Ь до Ь, по г от -с до с, достаточно применить матрицу масштабирования:
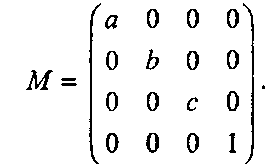
О Найдите обратную матрицу М~1 и докажите, что матрица эллипсоида равна
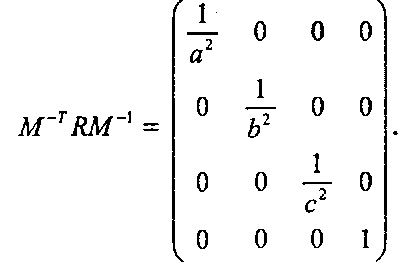
Напишите неявную форму для эллипсоида.
