Отметим, что обычно невозможно построить список граней по списку ребер и списку вершин. Рисунок 6.74 являет классический пример этого. Исходя из одного списка ребер, невозможно сказать, где находятся грани. Даже каркасная модель куба может представлять собой или закрытую, или открытую коробку. Следовательно, список граней содержит больше информации, нежели список ребер.

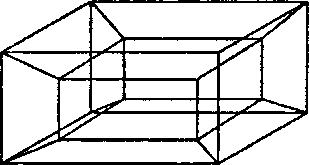
Рис. 6.74. Неоднозначный объект

Моделирование поверхностей полигональными сетками

Тематическое задание 6.8. Сводчатые потолки Уровень сложности III.

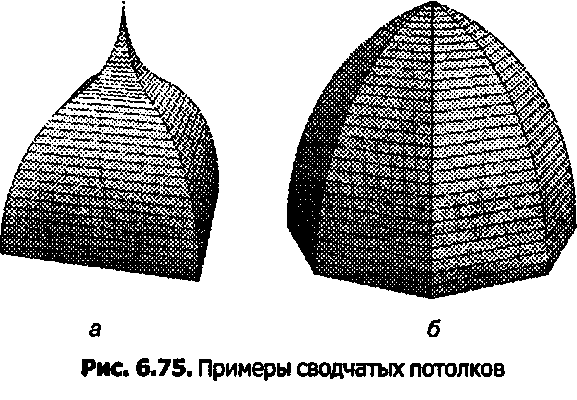
Многие классические здания имеют куполовидные потолки или крыши в форме свода (vault). На рис. 6.75, а приведен «сомкнутый свод», построенный на квадратном основании. Четыре «переборки», каждая из которых является линейчатой поверхностью, натянуты на дискретные «шаги» круговой развертки некоторой кривой и встречаются в вершине. Форма арки представляет собой «гусек» (ogee), приведенный на рис. 3.70. На рис. 6.75, б изображен сомкнутый свод, построенный на восьмиугольнике и имеющий восемь стенок. Эта арка является стрельчатой аркой, показанной на рис. 3.69. Напишите функцию, которая создает каркасную модель сводчатых куполов, построенных на квадрате и на октагоне.

Тематическое задание 6.9.0 Платоновых телах

Уровень сложности II.

Создайте файлы (в формате, описанном в тематическом задании 6.1) для каждого Платонова тела. Поэкспериментируйте с чтением каждого файла в приложение и с рисованием соответствующего объекта.

Тематическое задание 6.10. Об Архимедовых телах

Уровень сложности II.

Изображения всех 13 Архимедовых тел можно найти во многих источниках (например, [Kappraff, 121] и [Wenninger, 211]). Каждое Архимедово тело может быть сформировано посредством усечения одного из Платоновых тел, как это описано в разделе «Другие любопытные многогранники». Создайте файлы (в формате, описанном в тематическом задании 6.3) для каждого из следующих полиэдров"opengl1_453.html">⇐ Предыдущая| |Следующая ⇒